Consider the etch rate data in Exercise 10-23. (a) Test the hypothesis H 0 : Ï 2 1 = Ï 2 2 against H 1

Consider the etch rate data in Exercise 10-23.

(a) Test the hypothesis H₀: σ²₁ = σ²₂ against H₁: σ²₁ ‰  σ²₂ using α = 0.05, and draw conclusions.

(b) Suppose that if one population variance is twice as large as the other, you want to detect this with probability at least 0.90 (using α = 0.05). Are the sample sizes n₁ = n₂ = 10 adequate?

Exercise 10-23

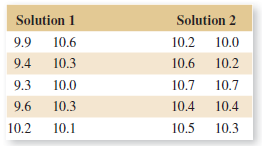
In semiconductor manufacturing, wet chemical etching is often used to remove silicon from the backs of wafers prior to metallization. The etch rate is an important characteristic in this process and known to follow a normal distribution. Two different etching solutions have been compared using two random samples of 10 wafers for each solution. The observed etch rates are as follows (in mils per minute):

(a) Construct normal probability plots for the two samples. Do these plots provide support for the assumptions of normality and equal variances? Write a practical interpretation for these plots.

(b) Do the data support the claim that the mean etch rate is the same for both solutions? In reaching your conclusions, use α = 0.05 and assume that both population variances are equal. Calculate a P-value.

(c) Find a 95% confidence interval on the difference in mean etch rates.

Solution 1 Solution 2 9.9 10.6 10.2 10.0 9.4 10.3 10.6 10.2 9.3 10.0 10.7 10.7 9.6 10.3 10.4 10.4 10.2 10.1 10.5 10.3