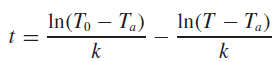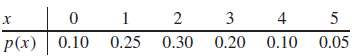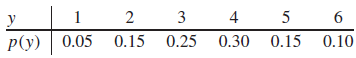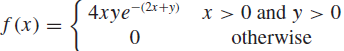Statistics For Engineers And Scientists 4th Edition William Navidi - Solutions

Discover comprehensive resources for "Statistics For Engineers And Scientists 4th Edition" by William Navidi. Access a wide array of expertly crafted answers and solutions, including a detailed solution manual and step-by-step answers to enhance your understanding. Our online platform features solved problems and a test bank, making it easier to tackle challenging questions and answers. Utilize the instructor manual and chapter solutions for in-depth insights. Enjoy the convenience of free download options for solutions PDF and textbook materials, providing invaluable support for mastering engineering statistics.