X 1 and S 2 1 are the sample mean and sample variance from a population with mean 1 and variance 1 2 .

X̅₁ and S²₁ are the sample mean and sample variance

from a population with mean μ1 and variance σ₁². Similarly,

X̅₂ and S₂² are the sample mean and sample variance from a

second independent population with mean μ₂ and variance σ₂².

The sample sizes are n₁ and n₂, respectively.

(a) Show that X₁ − X₂ is an unbiased estimator of μ₁ − μ₂.

(b) Find the standard error of X̅₁ − X̅₂. How could you estimate

the standard error?

(c) Suppose that both populations have the same variance; that

is, σ²₁ = σ²₂ = σ². Show that

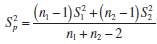
is an unbiased estimator of σ².

S = (m 1)S + (m 1)S m+m-2