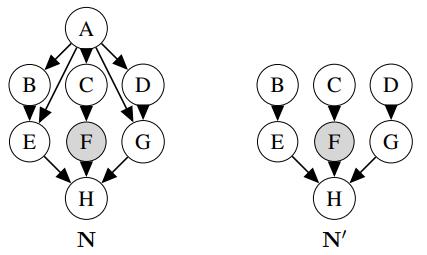
Question: a. Consider answering P(H | + f) by variable elimination in the Bayes nets N and N' shown in Figure S13.44, where the elimination order
a. Consider answering P(H | + f) by variable elimination in the Bayes nets N and N' shown in Figure S13.44, where the elimination order is alphabetical and all variables are binary. How large are the largest factors made during variable elimination for N and N' ?
b. Borrowing an idea from cutset conditioning in Chapter 6, we may be able to simplify variable elimination in N by instantiating some variables. Let’s pick an instantiation set to pretend to observe, and then do variable elimination with these additional instantiations.
Consider the original query P(H | + f), but let A be the instantiation set so A = a is observed. Now the query is H with observations F = + f, A = a.
(i) What is the size of the largest factor made during variable elimination with the A = a instantiation?
(ii) Given a Bayes net over n binary variables with k variables chosen for the instantiation set, how many instantiations of the set are there?
c. Let’s answer P(H | + f) by variable elimination with the instantiations of A.
(i) What quantity does variable elimination for P(H | + f) with the A = + a instantiation compute without normalization? That is, what is the last factor made by elimination?
(ii) Let I+(H) = F(H, +a, +f) and I−(H) = F(H, −a, +f) be the last factors made by variable elimination with instantiations A = + a and A = − a. How do we calculate the desired answer P(+h | + f)?
d. What is the time complexity of instantiated elimination, expressed in terms of n (the number of variables), k (the instantiation set size), f (the dimension of the largest factor made by elimination without instantiation), and i (the dimension of the largest factor made by elimination with instantiation)?
Figure S13.44
A B E F HZ N G B E C F H N' D G
Step by Step Solution
3.42 Rating (168 Votes )
There are 3 Steps involved in it
a i The largest factor made during variable elimination for N is fB C D E G after eliminating A It h... View full answer

Get step-by-step solutions from verified subject matter experts


