PacLabs has just created a new type of mini power pellet that is small enough for Pacman to carry around with him when he’s running around mazes. Unfortunately, these mini-pellets don’t guarantee that Pacman will win all his fights with ghosts, and they look just like the regular dots Pacman carries around to snack on.

Pacman just ate a snack (P), which was either a mini-pellet (+p), or a regular dot (−p), and is about to get into a fight (W), which he can win (+w) or lose (−w). Both these variables are unknown, but fortunately, Pacman is a master of probability. He knows that his bag of snacks has 5 mini-pellets and 15 regular dots. He also knows that if he ate a mini-pellet, he has a 70% chance of winning, but if he ate a regular dot, he only has a 20% chance. 

a. What is P(+w), the marginal probability that Pacman will win? 

b. Pacman won! Hooray! What is the conditional probability P(+p | +w) that the food he ate was a mini-pellet, given that he won? Pacman can make better probability estimates if he takes more information into account. First, Pacman’s breath, B, can be bad (+b) or fresh (−b). Second, there are two types of ghost (M): mean (+m) and nice (−m). Pacman has encoded his knowledge about the situation in the Bayes net in Figure S13.34. 

c. What is the probability of the atomic event (−m, +p, +w, −b), where Pacman eats a mini-pellet and has fresh breath before winning a fight against a nice ghost?

d. Which of the following conditional independence statements are guaranteed to be true by the Bayes net graph structure? 

(i) W ⊥⊥ B 

(ii) W ⊥⊥ B | P 

(iii) M ⊥⊥ P 

(iv) M ⊥⊥ P | W (v) M ⊥⊥ B 

(vi) M ⊥⊥ B | P 

(vii) M ⊥⊥ B | 

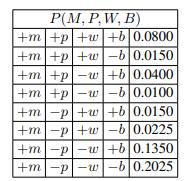
For the remainder of this question, use the half of the joint probability table that has been computed for you in Figure S13.35. e. What is the marginal probability, P(+m, +b) that Pacman encounters a mean ghost and has bad breath? 

f. Pacman observes that he has bad breath and that the ghost he’s facing is mean. What is the conditional probability, P(+w | +m, +b), that he will win the fight, given his observations? 

g. Pacman’s utility is +10 for winning a fight, -5 for losing a fight, and -1 for running away from a fight. Pacman wants to maximize his expected utility. Given that he has bad breath and is facing a mean ghost, should he stay and fight, or run away? Justify your answer numerically!

Figure S13.34

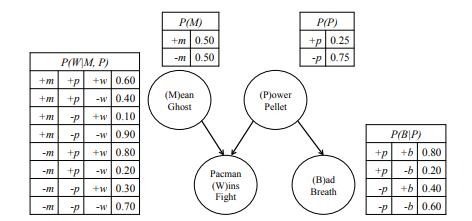
Figure S13.35

Transcribed Image Text:

P(WM, P) +m +p+w 0.60 +p -w 0.40 P+w0.10 P -w 0.90 -m+p+w 0.80 -m +p -w 0.20 -P +0.30 -P - 0.70 +m +m +m -m -m P(M) +m 0.50 -m 0.50 (M)ean Ghost Pacman (W)ins Fight (P)ower Pellet P(P) +p0.25 P0.75 (B)ad Breath P(BP) +p+b 0.80 +p -b 0.20 -P +b 0.40 -P -b 0.60