Question: Trace a data-driven execution of the financial advisor of Example 3.3.5 for the case of an individual with four dependents, $18,000 in the bank, and
Trace a data-driven execution of the financial advisor of Example 3.3.5 for the case of an individual with four dependents, $18,000 in the bank, and a steady income of $25,000 per year. Based on a comparison of this problem and the example in the text, suggest a generally, “best” strategy for solving the problem.
Data from Example 3.3.5
In the last example of Chapter 2 we used predicate calculus to represent a set of rules for giving investment advice. In that example, modus ponens was used to infer a proper investment for a particular individual. We did not discuss the way in which a program might determine the appropriate inferences. This is, of course, a search problem; the present example illustrates one approach to implementing the logic-based financial advisor, using goal-directed, depth-first search with backtracking. The discussion uses the predicates found in Section 2.4; these predicates are not duplicated here. Assume that the individual has two dependents, $20,000 in savings, and a steady income of $30,000. As discussed in Chapter 2, we can add predicate calculus expressions describing these facts to the set of predicate calculus expressions. Alternatively, the program may begin the search without this information and ask the user to add it as needed. This has the advantage of not requiring data that may not prove necessary for a solution. This approach, often taken with expert systems, is illustrated here. In performing a consultation, the goal is to find an investment; this is represented with the predicate calculus expression ∃ X investment(X), where X in the goal variable we seek to bind. There are three rules (1, 2, and 3) that conclude about investments, because the query will unify with the conclusion of these rules. If we select rule 1 for initial exploration, its premise savings_account(inadequate) becomes the subgoal, i.e., the child node that will be expanded next. In generating the children of savings_account(inadequate), the only rule that may be applied is rule 5. This produces the and node: amount_saved(X) ∧ dependents(Y) ∧ ¬ greater(X,minsavings(Y)). If we attempt to satisfy these in left-to-right order, amount_saved(X) is taken as the first subgoal. Because the system contains no rules that conclude this subgoal, it will query the user. When amount_saved(20000) is added the first subgoal will succeed, with unification substituting 20000 for X. Note that because and node is being searched, a failure here would eliminate the need to examine the remainder of the expression. Similarly, the subgoal dependents(Y) leads to a user query, and the response, dependents (2), is added to the logical description. The subgoal matches this expression with the substitution {2/Y}. With these substitutions, the search next evaluates the truth of ¬ greater (20000, minsavings(2)). This evaluates to false, causing failure of the entire and node. The search then backtracks to the parent node, savings_account(inadequate), and attempts to find an alternative way to prove that node true. This corresponds to the generation of the next child in the search. Because no other rules conclude this subgoal, search fails back to the top-level goal, investment(X). The next rule whose conclusions unify with this goal is rule 2, producing the new subgoals savings_account(adequate) ∧ income(adequate).
Continuing the search, savings account(adequate) is proved true as the conclusion of rule 4, and income(adequate) follows as the conclusion of rule 6. Although the details of the remainder of the search will be left to the reader, and/or graph that is ultimately explored appears in Figure 3.26.
Figure 3.26
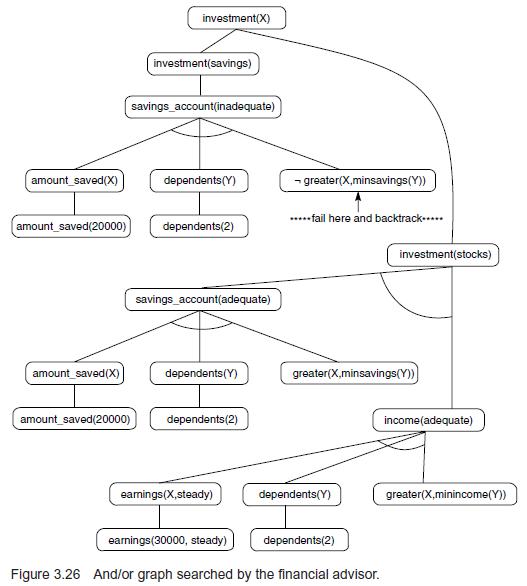
amount_saved(X) amount_saved(20000) amount_saved (X) investment(X) investment(savings) savings account(inadequate) dependents (Y) dependents (2) savings account(adequate) dependents (Y) amount_saved(20000) dependents (2) earnings (X,steady) greater(X,minsavings (Y)) .....fail here and backtrack..... greater(X,minsavings (Y)) dependents(Y) earnings (30000, steady) Figure 3.26 And/or graph searched by the financial advisor. investment(stocks) dependents (2) income (adequate) greater(X,minincome(Y))
Step by Step Solution
3.39 Rating (152 Votes )
There are 3 Steps involved in it
To trace a datadriven execution for the new case four dependents 18000 in savings and a steady income of 25000 lets follow how the expert system would ... View full answer

Get step-by-step solutions from verified subject matter experts


