Consider the following congestion network with origin and destination nodes \(o\) and \(d\), and an intermediate node \(v\). There are ten individual users who want to travel from \(o\) to \(d\).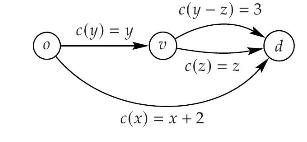

As shown, the cost on the bottom edge is \(c(x)=x+2\) when it has \(x\) users, where \(x+y=10\). The edge from \(o\) to \(v\) has cost function \(c(y)=y\). The top edge from \(v\) to \(d\) has constant cost 3 , and the lower edge from \(v\) to \(d\) has cost function \(c(z)=z\) if \(z\) of the \(y\) users use that edge, where \(0 \leq z \leq y\).

(a) Find all equilibria of this congestion game (note that \(x, y\) and \(z\) are integers), and their resulting average cost per user. [Hint: Consider first what \(z\) can be in an equilibrium.]

(b) For the same network, find the equilibrium when \(x, y, z\) can be fractional for a total flow of 10 from \(o\) to \(d\) (so this flow is now splittable). Compare its average cost with the costs of the equilibria in (a).

Transcribed Image Text:

c(y) = y 0 V c(y-z) = 3 c(z) = z c(x) = x+2 d