Consider the following congestion network with three nodes. As shown, an edge has the cost function \(c(x)=x\) if the flow (number of users) on that edge is \(x\), except for the edges \(v u\) and \(w u\) where \(c(x)=0\). The table on the right shows four users \(i=1,2,3,4\) with different origins \(o_{i}\) and destinations \(d_{i}\). In this network, each user has two possible routes from her origin to her destination.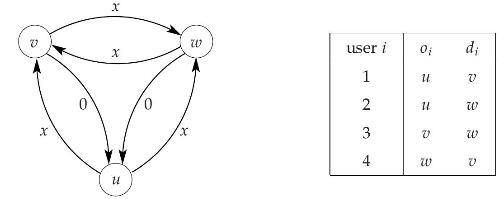

Find two equilibria of this congestion game, one with low cost and one with high cost. Explain why the equilibrium property holds in each case. Compare the costs of the two equilibria. What is the socially optimal (possibly non-equilibrium) flow?

d P 02 3 m user i 1 2 3 4 10 = 11 = x x P x x n