Consider the following \(3 \times 3\) game.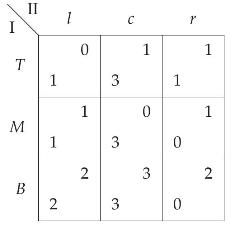

(a) Identify all pairs of strategies where one strategy weakly dominates the other.

(b) Assume you are allowed to remove a weakly dominated strategy of some player. Do so, and repeat this process (of iterated elimination of weakly dominated strategies) until you find a single strategy pair of the original game. (Remember that two payoff equivalent strategies do not weakly dominate each other!)

(c) Find such an iterated elimination of weakly dominated strategies that results in a strategy pair other than the one found in (b), where both strategies, and the payoffs to the players, are different.

(d) What are the equilibria (in pure strategies) of the game?

I T M II 1 1 1 C 0 1 1 3 B 2 2 r 1 1 3 0 3 2 3 0