Consider the following game on a rectangular board where a white and a black counter are placed in each row, like in this example: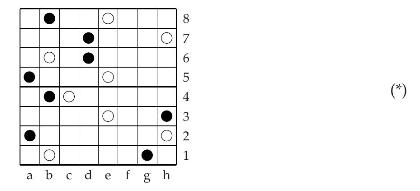

Player I is White and starts, and player II is Black. Players take turns. In a move, a player moves a counter of his color to any other square within its row, but may not jump over the other counter. For example, in (*) above, in row 8 White may move from \(\mathrm{e} 8\) to any of the squares \(\mathrm{c} 8, \mathrm{~d} 8, \mathrm{f} 8, \mathrm{~g} 8\), or h8. The player who can no longer move loses.

(a) Who will win in the following position?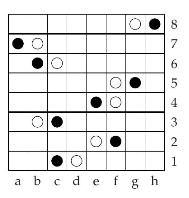

(b) Show that White can win in position (*) above. Give at least two winning moves from that position. Justify your answers.

87654321 07 a b c d e f g h (*)