Let \(G\) be the following game: Player I chooses a non-negative real number \(x\), and simultaneously player II chooses a non-negative real number \(y\). The resulting (symmetric) payoffs are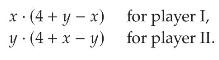

(a) Given \(x\), determine player II's best response \(y(x)\) (which is a function of \(x\) ), and player I's best response \(x(y)\) to \(y\). Find an equilibrium, and give the payoffs to the two players.

(b) Find an SPE of the commitment game (where player I moves first), and give the payoffs to the two players.

(c) Are the equilibria in

(a) and

(b) unique?

(d) Let \(G\) be a game where the best response \(y(x)\) of player II to any strategy \(x\) of player I is always unique. Show that in any SPE of the commitment game (where player I moves first), the payoff to player I is at least as large as his payoff in any equilibrium of the original game \(G\).

x (4+y-x) for player I, y (4+xy) for player II.