Show that if \(Y\) is a Markov chain on two states, then the off-diagonal elements of \(Y\), in their columns, are proportional to the probabilities of a stationary distribution \(x\) of \(Y\). That is, if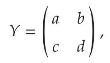

then \(\left(\begin{array}{ll}c & b\end{array}\right)=(c+b) x^{\top}\). Exactly when is \(x\) unique? Argue carefully.

9 Y = a C