For the dependent system of Example 8 on page 150, both equations can be written as y = 1/3x − 3. The solution for the system can then be shown in terms of a general point on the graph as (x, = 1/3x − 3). This is referred to as the solution with arbitrary x. Find the solutions in this form for this system for x = −3, and x = 9.

Data from Example 8

Solve the system of equations

x − 3y = 9

−2x + 6y = −18

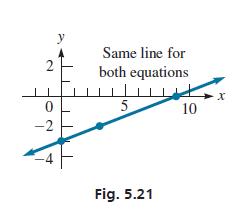
We find that the intercepts and a third point for the first line are (9, 0), (0, −3), and (3, −2). For the second line, we then find that the intercepts are the same as for the first line. We also find that the check point (3, −2) also satisfies the equation of the second line. This means that the two lines are really the same line. Another check is to write each equation in slope-intercept form. This gives us the equation y = 1/3x − 3 for each line. See Fig. 5.21.

2 0 -2 -4 y Same line for both equations 5 Fig. 5.21 10 X