In Example 2, change (2, 1) to (−2, 1).

Data from Example 2

Find the equation of the circle with center at (2, 1) and that passes through (4,−6). In Eq. (21.11), we can determine the equation of this circle if we can find h, k, and r. From the given information, the center is (2, 1), which means h = 2 and k = 1. To find r, we use the fact that all points on the circle must satisfy the equation of the circle. The point (4,−6) must satisfy Eq. (21.11), with h = 2 and k = 1. This means (4 − 2)² + (−6 − 1)² = r² or r² = 53. Therefore, the equation of the circle is 

(x − 2)² + (y − 1)² = 53 

This circle is shown in Fig. 21.32.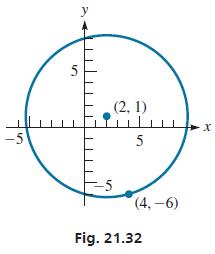

-5 5 (2, 1) 5 (4,-6) Fig. 21.32 X