Using the results of Example 5, find the cube roots of −125.

Data from Example 5

Find the cube root of −1. Because −1 is a real number, we can find its cube root by means of the definition. Since (−1)³ = −1, ³√−1 = −1. We check this by DeMoivre’s theorem. Writing −1 in polar form, we have −1 = 1(cos 180° + j sin 180°)

Applying DeMoivre’s theorem, with n = 1/3, we obtain

Observe that we did not obtain −1 as the answer. If we check the answer, in the form

by actually cubing it, we obtain −1! Therefore, it is a correct answer. We should note that it is possible to take 1/3 of any angle up to 1080° and still have an angle less than 360°. Because 180° and 540° have the same terminal side, let us try writing −1 as 1(cos 540° + j sin 540°). Using DeMoivre’s theorem, we have

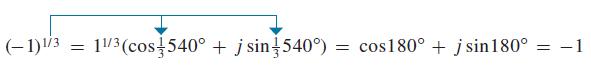
We have found the answer we originally anticipated. Angles of 180° and 900° also have the same terminal side, so we try

Checking this, we find that it is also a correct root. We may try 1260°, but 1/3(1260° = 420° which has the same functional values as 60°, and would give us the answer 0.5000 + 0.8660 j again. We have found, therefore, three cube roots of −1. They are 

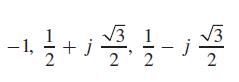
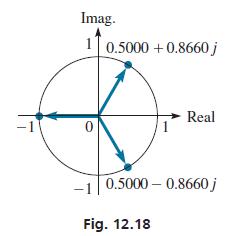
These roots are graphed in Fig. 12.18. Note that they are equally spaced on the circumference of a circle of radius 1.

Transcribed Image Text:

(-1)/3 = 11/3 (cos 180° + jsin 180°) = cos60° + j sin 60° = 1/2 +j/3³32 = = 0.5000+ 0.8660j exact answer decimal approximation