A window is broken in forcing entry to a house. The refractive index of a piece of glass found at the scene of the crime is x, which is supposed N(θ₁,ϕ). The refractive index of a piece of glass found on a suspect is y, which is supposed N(θ₂,ϕ). In the process of establishing the guilt or innocence of the suspect, we are interested in investigating whether H₀: θ₁ = θ₂ is true or not. The prior distributions of θ₁ and θ₂ are both N(µ,ψ) where >> ϕ. Write

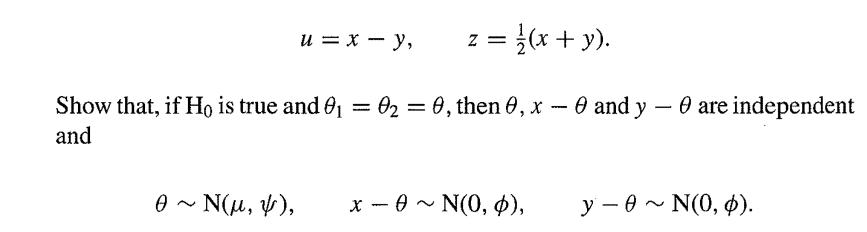
By writing u = (x - θ) - (y - θ) and z = θ + ½(x - θ) + ½(y - θ), go on to show that u has an N(0, 2ϕ) distribution and that z has an N(µ, ½ϕ + ψ) so approximately an N(µ, ψ) distribution. Conversely, show that if Ho is false and θ₁ and θ₂ are assumed independent, then θ₁, θ₂ , x - θ₁ and y - θ₂ are all independent and

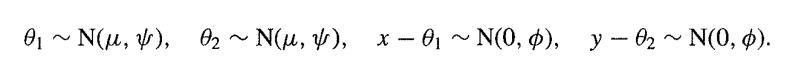
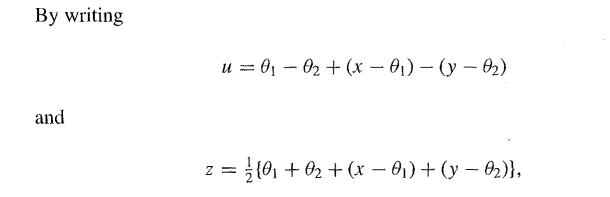
show that in this case u has an N(0, 2(ϕ + ψ)), so approximately an N(0, 2ψ),distribution, while z has an N(µ, ½ϕ + ψ)) , so approximately an N(µ,½ψ), distribution. Conclude that the Bayes factor is approximately 

Suppose that the ratio √ϕ/ψ of the standard deviations is 100 and that u = 2 x √(2∅), so that the difference between x and y represents two standard deviations, and that z = µ,, so that both specimens are of commonly occurring glass. Show that a classical test would reject H₀ at the 5% level, but that B = 9.51, so that the odds in favour of H₀ are multiplied by a factor just below 10.

z = 1/(x+y). Show that, if Ho is true and 0 = 0 = 0, then 0, x - 0 and y - and y - are independent and . ~ N(u, v), u = x - y, x-0~ N(0, 0), y-0~ N(0, 0).