By substituting in the form for the posterior density of the correlation coefficient and then expanding as a power series in u, show that the integral can be expressed as a series of beta functions Hence, deduce that where cosht pr 1 pr 1 u...

The Answer is in the image, click to view ...

By substituting in the form for the posterior density of the correlation coefficient and then expanding as

Question:

By substituting

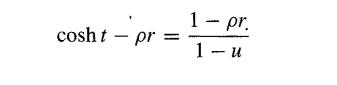
cosht - pr = 1 - pr. 1-u

in the form

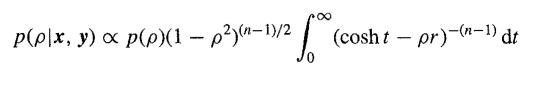$f. (0 p(p\x, y) x p(p)(1-p)(n-1)/2 (cosht - pr)-(n-1) dt$ for the posterior density of the correlation coefficient and then expanding

_[n(ad + 1) - 1] as a power series in u, show that the integral can be expressed as a series of beta functions. Hence, deduce that

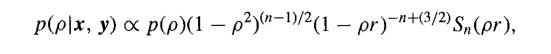
p(plx, y) x p(p)(1 - p)(n-1)/2(1 - pr)-n+(3/2) S (pr),

where

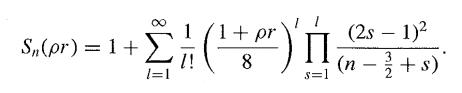
+(+) pr 8 Su(pr) =1+ (2s - 1) 3 (n = /+s) -

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Bayesian Statistics An Introduction

ISBN: 9781118332573

4th Edition

Authors: Peter M. Lee

See More Books

Question Posted: Nov 28, 2023 04:51 AM

See More Questions

2. Say the government levies a linear tax at rate t on all reported tax- able income. A representative agent decides on her labour supply (L) and how much income to shelter from taxation (e) through...
Let A be a square matrix. A square root of A is a matrix B of the same order such that B=A How to find a square root for a given matrix? If the matrix is symmetric, positive definite, there is a way...
Many microorganisms propel themselves, at low Reynolds number, using undulatory motion. Examples include the helical motion of E. colis corkscrew tail (Box 14.3), and undulatory waves in a forest of...
Look at the following code. Which line will cause a compiler error? Explain why. Line 1 public class ClassA Line 2 { Line 3 public ClassA () {} Line 4 public final int methodl (int a) () Line 5...
You are a member of the most popular student club on campus, the Accounting Antidefamation Organization. Recently, the field of accounting was savagely attacked in an article written by a militant...
Let H V Rn, with H convex and V open, and suppose that : V Rn is C1. a) Show that if E is a closed subset of H and then h(x)/||h|| 0 uniformly on E, as h 0. b) Show that if R is a closed...
Distinguish between verification and validation activities and how these activities support project quality management. AppendixLO1
A radioactive material produces 1280 decays per minute at one time, and 4.6h later produces 320 decays per minute. What is its half-life?
.. Optus 11:55 AM The author has locked parts of this Dismiss document. You can make cha... more d. It makes up a significant portion of a retailer's asets. 6 QB 3. The business completes a purchase...
Fill in the details of the derivation of the prior from Jeffreys' rule as outlined at the end of Section 6.1. p(0, V, p) x (v)- (1-)-3/2
By writing and using repeated integration by parts, show that the posterior distribution of p can be expressed as a finite series involving powers of and Student's t integrals. w(w+w-2pr)-(n-1) =...
_____________ is an uncertainty that can have a negative or positive effect on meeting project objectives. a. Risk utility b. Risk tolerance c. Risk management d. Risk LO.1
5) A frictionless rod of length L rotates counterclockwise in the with constant angular speed w at an angle a to the z axis. A bead of mass m, free to slide on the rod, leaves the origin with initial...
1) Louisa is a corn farmer in Illinois. She anticipates a harvest in August of 3 million bushels of yellow corn. Today is May. Louise plans to hedge her sale of corn in August using corn futures...
2. DETAILS MY NOTES In a statistical test, we have a choice of a left-tailed test, a right-tailed test, or a two-tailed test. Is it the null hypothesis or the alternate hypothesis that determines...
2. The model of a two-story building shown in Figure 2. The girders are assumed to be rigid, and the columns have flexural rigidities EI and EI2, with negligible masses. The stiffness of each column...
Prepare journal entries to record these transactions. (List all debit entries before credit entries. Credit account titles are automatically indented when amount is entered. Do not indent manually....
Match the statement to interphase or the phase of mitosis in the key. Key a. Metaphase b. Interphase c. Telophase d. Prophase e. Anaphase Centromere splits and sister chromosomes move to opposite...
Evaluate the line integral, where C is the given curve. C x 2 dx + y 2 dy, C consists of the arc of the circle x 2 + y 2 = 4 from (2, 0) to (0, 2) followed by the line segment from (0, 2) to (4, 3)
You operate a small hardware store with emphasis on manufacturer brands and have barely been breaking even. Evaluate the proposal of a large wholesaler that offers a full line of dealer-branded...
Give an example where packaging costs probably ( a ) lower total distribution costs and ( b ) raise total distribution costs.
How would the marketing mix for a staple convenience product differ from the one for a homogeneous shopping product? How would the mix for a specialty product differ from the mix for a heterogeneous...
Suppose I have computed the cost of carbon per mile for my car at 0 . 0 1 2 per mile. Assume that the interest rate is 4 % and that I drive the car 2 8 , 0 0 0 miles per year. What is the present...
Imagine that in stable growth period, the firm earns ROIC of 10% and has after tax EBIT of 200 and reinvestment $ of 40. What is the steady state growth rate? 20% O 10% 2%
Tanner-UNF Corporation acquired as a long-term investment $160 million of 5.0% bonds, dated July 1, on July 1, 2021. Company management has the positive intent and ability to hold the bonds until...

By substituting in the form for the posterior density of the correlation coefficient and then expanding as

Question:

cosht - pr = 1 - pr. 1-u

Step by Step Answer:

Bayesian Statistics An Introduction

Students also viewed these Business questions