Many microorganisms propel themselves, at low Reynolds number, using undulatory motion. Examples include the helical motion of

Question:

Many microorganisms propel themselves, at low Reynolds number, using undulatory motion. Examples include the helical motion of E. coli’s corkscrew tail (Box 14.3), and undulatory waves in a forest of cilia attached to an organism’s surface, or near a bare surface itself. As a 2-dimensional model for locomotion via surface waves, we idealize the organism’s undisturbed surface as the plane y = 0, and we assume the surface undulates in and out with displacement δy = (−u/kC) sin[k(x − Ct)] and hence velocity V_y = u cos[k(x − Ct)]. Here u is the amplitude, k the wave number, and C the surface speed in the organism’s rest frame. Derive the velocity field v for the fluid at y > 0 produced by this wall motion, and from it deduce the velocity of the organism through the fluid. You could proceed as follows.

(a) The velocity field must satisfy the incompressible, low-Reynolds-number equations ∇P = η∇²v and ∇ · v = 0 [Eqs. (14.20) and (14.21)]. Explain why v (which must point in the x and y directions) can be expressed as the curl of a vector potential that points in the z direction: v = ∇ × (ζ e_z); and show that ζ(t , x, y) satisfies the biharmonic equation: ∇²∇²ζ = 0.

(b) Show that the following ζ satisfies the biharmonic equation and satisfies the required boundary conditions at the organism’s surface, vx[x, δy(x, t), t]= 0and v_y[x, δy(x, t), t]= V_y(x, t), and the appropriate boundary conditions at y→∞:

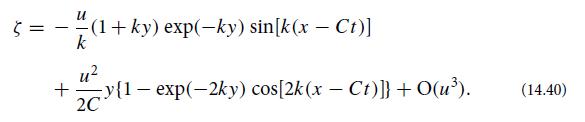
Explain how ∇P = η∇²v is then easily satisfied.

(c) Show that the streamlines (tangent to v) are surfaces of constant ζ. Plot these streamlines at t = 0 and discuss how they change as t passes. Explain why they are physically reasonable.

(d) Show that at large y the fluid moves with velocity v = [u²/(2C)]e_x, and that therefore, in the asymptotic rest frame of the fluid, the organism moves with velocity −[u²/(2C)]e_x, opposite to k. Is this physically reasonable? Why does the organism’s inertia (and hence its mass) not influence this velocity? That the organism’s velocity is second order in the velocity of its surface waves illustrates the difficulty of locomotion at low Reynolds number.

(e) Now consider what happens if the undulation is longitudinal with motion lying in the plane of the undulating surface. Sketch the flow pattern, and show that the organism will now move in the direction of k.

[Eqs. (14.20) and (14.21)