Consider an experiment E = {X, , p(xl)}. We say that censoring (strictly speaking, fixed censoring) occurs
Question:
Consider an experiment E = {X̃, θ, p(xlθ)}. We say that censoring (strictly speaking, fixed censoring) occurs with censoring mechanism g (a known function of X̃) when, instead of X̃, one observes y = g(x). A typical example occurs when we report x if x g = {ỹ, θ, p(ylθ)}. A second method with censoring mechanism his said to be equivalent to the first when
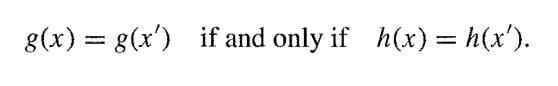
As a special case, if g is one-to-one then the mechanism is said to be equivalent to no censoring. Show that if two censoring mechanisms are equivalent, then the likelihood principle implies that
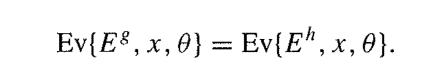
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





