Writing for the least squares and ridge regression estimators for regression coefficients , show that while its variance covariance matrix is Deduce expressions for the sum of the squares of the biases and for the sum of the variances of the regression coefficients, and hence show that the mean squ...

The Answer is in the image, click to view ...

Writing for the least-squares and ridge regression estimators for regression coefficients , show that while its variance-covariance

Question:

Writing

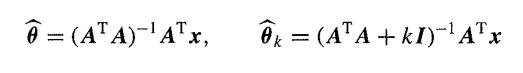
= (AA)-Ax, k = (AA+kI)Ax

for the least-squares and ridge regression estimators for regression coefficients θ, show that

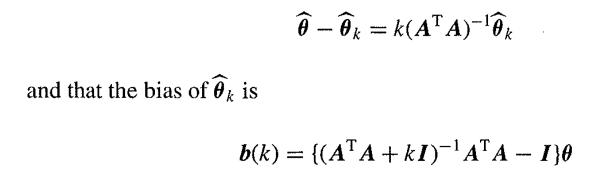
and that the bias of k is k = k(AA)-k - b(k) = {(AA+kI)AA 1}0 -

while its variance-covariance matrix is

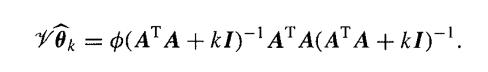
Vk = Q(AA+kI)AA(AA+KI).

Deduce expressions for the sum /of the squares of the biases and for the sum of the variances of the regression coefficients, and hence show that the mean square error is

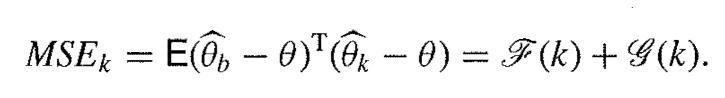
MSEK = E(0-0) (k 0) = F(k) + G(k).

Assuming thatis continuous and monotonic decreasing with (0) = 0 and that is continuous and monotonic increasing with = '(k) = 0, deduce that there always exists a k such that MSE_k 0 (Theobald, 1974).