Exercise 2.14 (Chebyshevs Inequality) Suppose that a random variable X has the mean = E[X] and the variance 2 = V[X]. For any

Exercise 2.14 (Chebyshev’s Inequality) Suppose that a random variable X has the mean μ = E[X] and the variance σ² = V[X]. For any ε > 0, prove that

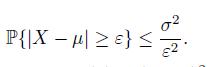
Hint: Use Markov’s inequality with h(x) = (x − μ)² and a = ε².

P{|X->}