Exercise 5.8 In the risk exchange market considered in Section 5.4, suppose that the expected utility is given by

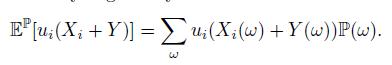
Suppose further that there is η > 0 such that π(Y ) = EP[ηY ] and EP[η] = 1, and that the utility functions are exponential (u′
i(x) = e−λix). Consider then the Lagrange equation

Prove the following.
(1) Calculate the first-order condition with respect to Y (ω) to maximize L, and show that

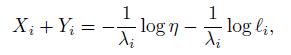
where Yi is the optimal risk exchange.
(2) Show that the market clearing condition implies

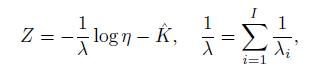
for some ˆK .
(3) Show that η = Ke−λZ and K = (EP[e−λZ])−1.
For the general case, see B¨uhlmann (1983) and Iwaki, Kijima, and Morimoto (2001).

Transcribed Image Text:

Eu(X + Y)]=ui(Xi(w)+Y(w))P(w). 3