Write a program that computes the spherical distance between two points on the surface of the Earth, given their latitudes and longitudes. This is a useful operation because it tells you how far apart two cities are if you multiply the distance by the radius of the Earth, which is roughly

Let φ₁, λ₁, and φ2, λ2 be the latitude and longitude of two points, respectively. Δλ the longitudinal difference, and Δσ the angular difference/distance in radians, can be determined as follows from the spherical law of cosines:

△σ = arccos(sinφ1sinφ2 + cosφ2cosφ2cos △λ)

For example, consider the latitude and longitude of two major cities:

Nashville, TN: N 36∘7.2',W 86∘40.2'

Los Angeles, CA: N 33∘56.4',W 118∘24.0'

You must convert these coordinates to radians before you can use them effectively in the formula. After conversion, the coordinates become

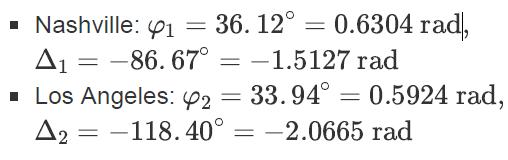
Using these values in the angular distance equation, you get

r△σ = 6372.795 × 0.45306 = 2887.259 km

Thus, the distance between these cities is about 2887 km, or 1794 miles.

Nashville: Y1 36. 12 0.6304 rad, A1 = -86. 67 = -1.5127 rad Los Angeles: 42 A2 = -118.40 33.94 = 0.5924 rad, %3D :-2.0665 rad