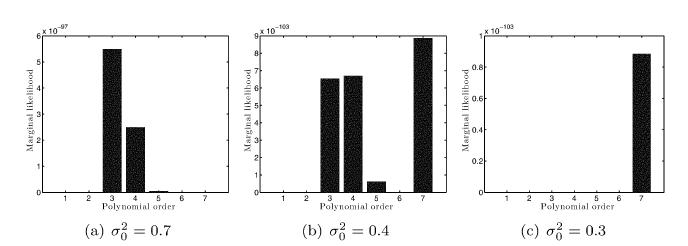
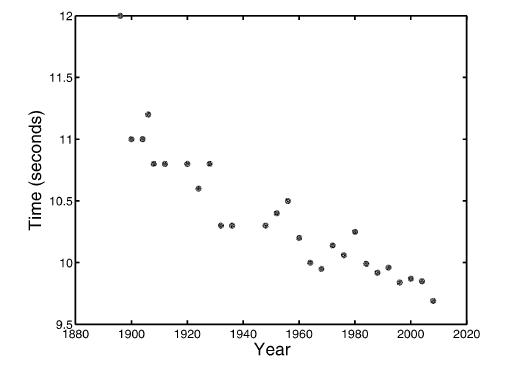
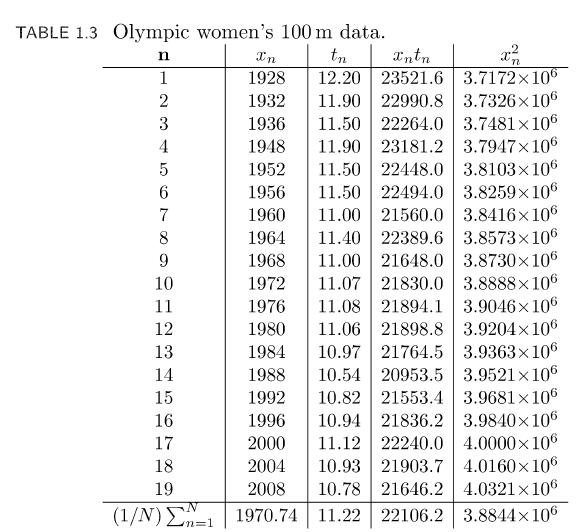
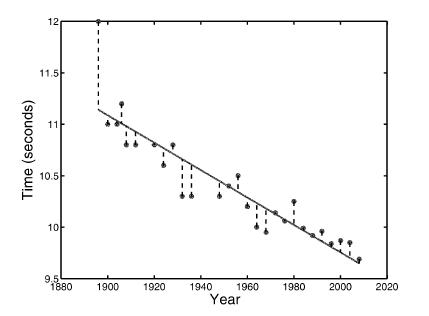
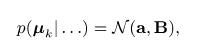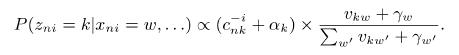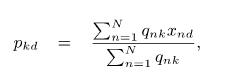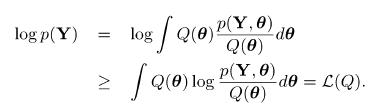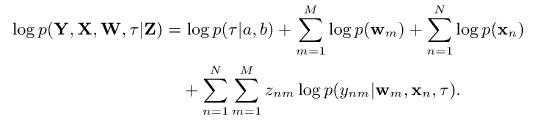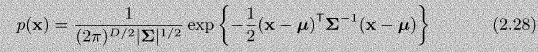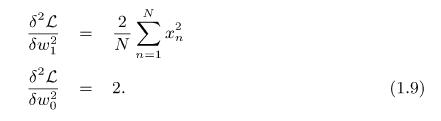A First Course In Machine Learning 2nd Edition Simon Rogers , Mark Girolam - Solutions

Discover comprehensive solutions and step-by-step answers to the questions from "A First Course In Machine Learning 2nd Edition" by Simon Rogers and Mark Girolam. Our online platform offers a complete solutions manual and answers key in a convenient PDF format, perfect for students and instructors alike. Explore chapter solutions and a detailed test bank to enhance your learning experience. Download the instructor manual for free and access solved problems to deepen your understanding of this essential textbook. Unlock the potential of machine learning with our expertly crafted questions and answers resource.

For some one-dimensional input data, construct a GP RBF covariance matrix. Use Gibbs sampling to sample functions from this GP prior (samples from a GP prior are just samples from a multivariate Gaussian). Compare the samples with values obtained by sampling directly from the Gaussian. In
Use Metropolis-Hastings instead of Gibbs sampling to sample from the GP classification model. Note that you will no longer need to perform the auxiliary variable trick. Compare the predictions with those obtained from the Gibbs sampling approach.
Using the provided code for performing Gibbs sampling for binary GP classification, compute the \(\hat{R}\) value for one of the training latent function values. How many samples need to be drawn before \(\hat{R}\) is lower than 1.01 ?
For the same GP model as in Exercise 9.3 , compute the autocorrelation of one of the training latent function values. How much thinning would be required to obtain independent samples?Data from Exercise 9.3Using the provided code for performing Gibbs sampling for binary GP classification, compute
Generate a regression dataset by sampling a function from a GP prior and then adding some noise. Use ABC to sample from the posterior. Each sample should be generated by first sampling from the GP prior and then adding noise. Use the Euclidean distance between the generated data and the original
For the mixture model where each component is a one-dimensional Gaussian with variance 1 , show that the conditional distribution for the mean of the \(k\) th mixture component is that given by Equation 10.4 .Data from Equation 10.4 P()N(a, B),
Implement the Gibbs sampler for the mixture model. Compute \(\hat{R}\) and the autocorrelation of the component means \(\mu_{k}\). How many samples are required for convergence? How much should the samples be thinned?
Marginalise the Gaussian mean from the Gibbs sampler to give a conditional distribution for \(z_{n k}\) conditioned only on the other assignments and the prior parameters \(\left(\mu_{0}, \boldsymbol{\Sigma}_{0}, \alpha\right)\).
Implement the collapsed Gibbs sampler for the Gaussian mixture model. At each iteration in the sampler, sample the means \(\mu_{k}\) even though they are not needed (sample them from the posterior you computed to marginalise them). Compare the autocorrelation and \(\hat{R}\) for the \(\mu_{k}\)
Implement a sampler that samples from the Chinese restaurant process. Repeatedly resample assignment of customers to tables and plot a histogram over the number of tables. Investigate how the histogram changes as you change \(\alpha\).
Write some code that will sample from a Dirichlet process. The code should store all previous samples and then copy previous samples or draw new samples from the base. Experiment with different base distributions and concentration parameters.
Using the MATLAB script provided (MATLAB script: hdp.m), experiment with setting the values of the concentration parameters for the top level DP \((\alpha)\) and the lower DPs \(\left(\gamma_{1}, \ldots, \gamma_{J}\right)\).
Derive a Gibbs sampling scheme for inference in the Hierarchical Dirichlet process. Assume that the base distribution is Gaussian \(\left(H=\mathcal{N}\left(\mu_{0}, \sigma_{0}^{2}\right)\right)\) and the observations are one-dimensional real values.
Derive the collapsed Gibbs sampler for LDA given in Equation 10.13 .Data from Equation 10.13 = k|xni = w,...) x (Ck+k) P(zni = kani Vkw + Tw w' Vkw' + Yw'
Write some code to sample from a GP prior. In particular, define some onedimensional input points ( \(x\) ), compute the covariance matrix by computing the covariance function at all pairs of points in \(x\) and then sample from the multivariate Gaussian with zero mean and covariance equal to the
Use a numerical optimisation routine to find the values of \(\sigma^{2}\) and \(\gamma\) that maximise the marginal likelihood for GP regression using an RBF covariance matrix (with \(\alpha=1\) ). Use data generated from a GP. How close are the optimised parameters to their true values?
For some one-dimensional input data ( \(x\) ), generate a real-valued latent function using a GP prior with an RBF covariance function. For each value, sample a random integer from a Poisson distribution with rate \(\lambda=\exp (f)\), i.e. the probability of getting the value \(z\) is equal
Use Metropolis-Hastings to perform inference in the binary GP classifier. The MH sampler should repeatedly resample values of \(\mathbf{f}\). For each sample, do a noise-free regression to compute \(f^{*}\) and then feed this through the logistic function to get a probability sample.
Given the expression for the area of a circle, \(A=\pi r^{2}\), and using only uniformly distributed random variates, devise a sampling approach for computing \(\pi\).
Rearrange the logistic function\[P\left(T_{\text {new }}=1 \mid \mathbf{x}_{\text {new }}, \widehat{\mathbf{w}}\right)=\frac{1}{1+\exp \left(-\widehat{\mathbf{w}}^{\top} \mathbf{x}_{\text {new }}\right)}\]to show that \(P\left(T_{\text {new }}=1 \mid \mathbf{x}_{\text {new }},
Assume that we observe \(N\) vectors of attributes, \(\mathbf{x}_{1}, \ldots, \mathbf{x}_{N}\) and associated integer counts \(t_{1}, \ldots, t_{N}\). A Poisson likelihood would be suitable:\[p\left(t_{n} \mid \mathbf{x}_{n}, \mathbf{w}\right)=\frac{f\left(\mathbf{x}_{n} ; \mathbf{w}\right)^{t_{n}}
Assuming \(\boldsymbol{\Sigma}_{c}=\mathbf{I}\) for all classes, compute the posterior density \(p\left(\boldsymbol{\mu}_{c} \mid \mathbf{X}^{c}\right)\) for the parameter \(\boldsymbol{\mu}_{c}\) of a Bayesian classifier where the set of training objects in class \(c\) is given by
Using the posterior computed in the previous exercise, compute the expected likelihood:\[p\left(\mathbf{x}_{\text {new }} \mid T_{\text {new }}=c, \mathbf{X}, \mathbf{t}\right)=\mathbf{E}_{p\left(\boldsymbol{\mu}_{c}, \boldsymbol{\Sigma}_{c} \mid
For a Bayesian classifier with multinomial class-conditionals with \(M\) dimensional parameters \(\mathbf{q}_{c}\), compute the posterior Dirichlet for class \(c\) when the prior over \(\mathbf{q}_{c}\) is a Dirichlet with constant parameter \(\alpha\) and the observations belonging to class \(c\)
Using the posterior computed in the previous exercise, compute the expected likelihood:\[p\left(\mathbf{x}_{\text {new }} \mid T_{\text {new }}=c, \mathbf{X}, \mathbf{t}\right)=\mathbf{E}_{p\left(\mathbf{q}_{c} \mid \mathbf{X}^{c}\right)}\left\{p\left(\mathbf{x}_{\text {new }} \mid
Derive the dual optimisation problem for a soft margin SVM.
Derive the EM update for the variance of the \(d\) th dimension and the \(k\) th component, \(\sigma_{k d}^{2}\), when the cluster components have a diagonal Gaussian likelihood\[p\left(\mathbf{x}_{n} \mid z_{n k}=1, \mu_{k 1}, \ldots, \mu_{K D}, \sigma_{k 1}^{2}, \ldots, \sigma_{k
Repeat Exercise 6.1 with isotropic Gaussian components:\[p\left(\mathbf{x}_{n} \mid z_{n k}=1, \boldsymbol{\mu}_{k}, \sigma_{k}^{2}\right)=\prod_{d=1}^{D} \mathcal{N}\left(\mu_{k d}, \sigma_{k}^{2}\right)\]Data from Exercise 6.1Derive the EM update for the variance of the \(d\) th dimension and the
Derive the EM update expression for the parameter \(p_{k d}\) given in Equation 6.22 .Data from Equation 6.22 Pkd N -1 gnkind N
Derive the MAP EM update expression for the parameter \(p_{k d}\) given in Equation 6.22 .Data from Equation 6.22 Pkd N -1 gnkind N
Derive the MAP update for a mixture model with Gaussian components that are independent over the \(D\) dimensions\[p\left(\mathbf{x}_{n} \mid z_{n k}=1, \mu_{k 1}, \ldots, \mu_{K D}, \sigma_{k 1}^{2}, \ldots, \sigma_{k D}^{2}\right)=\prod_{d=1}^{D} \mathcal{N}\left(\mu_{k d}, \sigma_{k
Show that the bound given in Equation 7.6 is maximised (i.e. equal to the true \(\log\) marginal likelihood) when \(Q(\boldsymbol{\theta})\) is identical to the true posterior \(p(\boldsymbol{\theta} \mid \mathbf{X})\).Data from Equation 7.6 log p(Y) = IV log/Q(6) P(Y, 0) Q(0) p(Y, 0) Q(0) log Q(0)
Compute the components of the variational posterior for the probabilistic PCA model with missing values described by Equation 7.15 .Data from Equation 7.15 M N log p(Y, X, W, Z) = log p(T|a, b) + log p(Wm) + log p(xn) N M m=1 n=1 +nm log pynm|Wm, Xn, T). n=1 m=1
For \(\alpha, \beta=1\), the beta distribution becomes uniform between 0 and 1 . In particular, if the probability of a coin landing heads is given by \(r\) and a beta prior is placed over \(r\), with parameters \(\alpha=1, \beta=1\), this prior can be written as\[p(r)=1 \quad(0 \leq r \leq
Repeat the previous exercise for the following prior, also a particular form of the beta density:\[p(r)=\left\{\begin{array}{cl} 2 r & 0 \leq r \leq 1 \\ 0 & \text { otherwise } \end{array}\right.\]What are the values of the prior parameters \(\alpha\) and \(\beta\) that result in \(p(r)=2 r\)
Repeat the previous exercise for the following prior (again, a form of beta density):\[p(r)=\left\{\begin{array}{cc} 3 r^{2} & 0 \leq r \leq 1 \\ 0 & \text { otherwise } \end{array}\right.\]What are the prior parameters here?Data from previous exerciseRepeat the previous exercise for the
At a different stall, you observe 20 tosses of which 9 were heads. Compute the posteriors for the three scenarios, the probability of winning in each case and the marginal likelihoods.
Use MATLAB to generate coin tosses where the probability of heads is 0.7 . Generate 100 tosses and compute the posteriors for the three scenarios, the probabilities of winning and the marginal likelihoods.
In Section 3.8 .4 we derived an expression for the Gaussian posterior for a linear model within the context of the Olympic \(100 \mathrm{~m}\) data. Substituting \(\boldsymbol{\mu}_{0}=\) \([0,0, \ldots, 0]^{\top}\), we saw the similarity between the posterior
Redraw the graphical representation of the Olympic \(100 \mathrm{~m}\) model to reflect the fact that the prior over \(\mathbf{w}\) is actually conditioned on \(\boldsymbol{\mu}_{0}\) and \(\boldsymbol{\Sigma}_{0}\).
In Figure 3.25 we studied the effect of reducing \(\sigma_{0}^{2}\) on the marginal likelihood. Using MATLAB, investigate the effect of increasing \(\sigma_{0}^{2}\).Data from Figure 3.25 Marginal likelihood -97 x10 1 2 3 4 5 Polynomial order (a) = 0.7 Marginal likelihood 8 -100 10 6 1 2 3 4 5 B
When performing a Bayesian analysis on the Olympics data, we assumed that the prior was known. If a Gaussian prior is placed on \(\mathbf{w}\) and an inverse gamma prior on the variance \(\sigma^{2}\)\[p\left(\sigma^{2} \mid \alpha,
By examining Figure 1.1 estimate the kind of values we should expect for \(w_{0}\) and \(w_{1}\) (e.g. High? Low? Positive? Negative?).Data from Figure 1.1 Time (seconds) 10.5 101 12 11.5- 9.5 1880 1900 1920 1940 1960 1980 2000 2020 Year
Write a MATLAB script that can find \(w_{0}\) and \(w_{1}\) for an arbitrary dataset of \(x_{n}, t_{n}\) pairs.
Show that\[\mathbf{w}^{\top} \mathbf{X}^{\top} \mathbf{X} \mathbf{w}=w_{0}^{2}\left(\sum_{n=1}^{N} x_{n 1}^{2}\right)+2 w_{0} w_{1}\left(\sum_{n=1}^{N} x_{n 1} x_{n 2}\right)+w_{1}^{2}\left(\sum_{n=1}^{N} x_{n 2}^{2}\right)\]where\[\mathbf{w}=\left[\begin{array}{l} w_{0} \\ w_{1}
Using \(\mathbf{w}\) and \(\mathbf{X}\) as defined in the previous exercise, show that \((\mathbf{X} \mathbf{w})^{\top}=\mathbf{w}^{\top} \mathbf{X}^{\top}\) by multiplying out both sides.
When multiplying a scalar by a vector (or matrix), we multiply each element of the vector (or matrix) by that scalar. For \(\mathbf{x}_{n}=\left[x_{n 1}, x_{n 2}\right]^{\top}, \mathbf{t}=\left[t_{1}, \ldots, t_{N}\right]^{\top}\), \(\mathbf{w}=\left[w_{0}, w_{1}\right]^{\top}\)
Using the data provided in Table 1.3 , find the linear model that minimises the squared loss.Data from Table 1.3 TABLE 1.3 Olympic women's 100 m data. n xn 1 1928 tn Intn 12.20 23521.6 3.7172106 x 2 1932 11.90 22990.8 3.7326106 3 1936 11.50 22264.0 3.7481x106 4 1948 11.90 23181.2 3.7947106 5 1952
Load the data stored in the file synthdata.mat. Fit a fourth-order polynomial function \(-f(x ; \mathbf{w})=w_{0}+w_{1} x+w_{2} x^{2}+w_{3} x^{3}+w_{4} x^{4}-\) to this data. What do you notice about \(w_{2}\) and \(w_{4}\) ? Use 10 -fold cross-validation to choose the polynomial order (between 1
Derive the optimal least squares parameter value, \(\widehat{\mathbf{w}}\), for the total training loss\[\mathcal{L}=\sum_{n=1}^{N}\left(t_{n}-\mathbf{w}^{\top} \mathbf{x}_{n}\right)^{2}\]How does the expression compare with that derived from the average loss?
The following expression is known as the weighted average loss:\[\mathcal{L}=\frac{1}{N} \sum_{n=1}^{N} \alpha_{n}\left(t_{n}-\mathbf{w}^{\top} \mathbf{x}_{n}\right)^{2}\]where the influence of each data point is controlled by its associated \(\alpha\) parameter. Assuming that each \(\alpha_{n}\)
Using \(K\)-fold cross-validation, find the value of \(\lambda\) that gives the best predictive performance on the Olympic men's \(100 \mathrm{~m}\) data for (a) a firstorder polynomial (i.e. the standard linear model) and (b) a fourth-order polynomial.
Would the errors in the \(100 \mathrm{~m}\) linear regression (shown in Figure 2.1 ) be best modelled with a discrete or continuous random variable?Data from Figure 2.1 Time (seconds) 12 11.5 10.5 10 111 9.5 1880 1900 1920 1940 1960 1980 2000 2020 Year
By using the fact that, when rolling a die, all outcomes are equally likely and by using the constraints given in Equations 2.1 and 2.2 , compute the probabilities of the dice landing with each of the six faces facing up. 0P(Y) 1, (2.1) P(Y = y) = 1 (2.2)
\(Y\) is a random variable that can take any positive integer value. The likelihood of these outcomes is given by the Poisson pdf\[p(y)=\frac{\lambda^{y}}{y!} \exp \{-\lambda\}\]By using the fact that, for a discrete random variable, the pdf gives the probabilities of the individual events
Assume that \(p(\mathbf{w})\) is the Gaussian pdf for a \(D\)-dimensional vector \(\mathbf{w}\) given in Equation 2.28 . By expanding the vector notation and rearranging, show that using \(\boldsymbol{\Sigma}=\sigma^{2} \mathbf{I}\) as the covariance matrix assumes independence of the \(D\)
Using the same setup as Exercise 2.5 above, see what happens if we use a diagonal covariance matrix with different elements on the diagonal, i.e.\[\boldsymbol{\Sigma}=\left[\begin{array}{cccc} \sigma_{1}^{2} & 0 & \ldots & 0 \\ 0 & \sigma_{2}^{2} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots
Show that for a first-order polynomial, the diagonal elements of the Hessian matrix of second derivatives of the log-likelihood is equivalent to (they will differ by a multiplicative constant) the second derivatives in Equation 1.9 .Data from Equation 1.9 82L 82L 2. N n=1 (1.9)
Assume that a dataset of \(N\) values, \(x_{1}, \ldots, x_{N}\), was sampled from a Gaussian distribution. Assuming that the data are IID, find the maximum likelihood estimate of the Gaussian mean and variance. (start by writing down the combined likelihood of all \(N\) data points and note that
Assume that a dataset of \(N\) binary values, \(x_{1}, \ldots, x_{N}\), was sampled from a Bernoulli. Compute the maximum likelihood estimate for the Bernoulli parameter.
Obtain the maximum likelihood estimates of the mean vector and covariance matrix of a multivariate Gaussian density given \(N\) observations \(\mathbf{x}_{1}, \ldots, \mathbf{x}_{N}\).
Show that the maximum likelihood estimate of the noise variance in our linear model,\[\widehat{\sigma^{2}}=\frac{1}{N}\left(\mathbf{t}^{\top} \mathbf{t}-\mathbf{t}^{\top} \mathbf{X} \widehat{\mathbf{w}}\right)\]can also be expressed as\[\widehat{\sigma^{2}}=\frac{1}{N}

A First Course In Machine Learning 2nd Edition Simon Rogers , Mark Girolam - Solutions

Step by Step Answers