Assume that \(p(\mathbf{w})\) is the Gaussian pdf for a \(D\)-dimensional vector \(\mathbf{w}\) given in Equation 2.28 . By expanding the vector notation and rearranging, show that using \(\boldsymbol{\Sigma}=\sigma^{2} \mathbf{I}\) as the covariance matrix assumes independence of the \(D\) elements of \(\mathbf{w}\). You will need to be aware that the determinant of a matrix that only has entries on the diagonal \(\left(\left|\sigma^{2} \mathbf{I}\right|\right)\) is the product of the diagonal values and that the inverse of the same matrix is constructed by simply inverting each element on the diagonal. (a product of exponentials can be expressed as an exponential of a sum.)

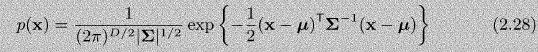
1 p(x)= exp (2)/2| 1/2 (2.28)