A well-studied optimization problem is the traveling salesperson problem (TSP). Given travel distances between N cities, the TSP problem is to construct a tour that has minimal total distance traveled.

A tour is defined as a loop that contains all N cities in which you enter and leave each city once, and return home to the city in which you began. The asymmetric traveling salesperson problem refers to the data not being symmetric, that is, the distance from city A to city B is not necessarily the same as the distance from city B to city A. The TSP problem is difficult to solve to optimality because integer-programming-

based methods result in subtours forming rather than one large tour.

However, a heuristic approach using the INDEX function in Excel with the Evolutionary method and a special constraint called “All Different” can yield good solutions. The “All Different” constraint ensures that the decision variables each take on a different integer value.

The file atsp contains a matrix with the distances in miles between 15 cities and a model for solving the associated TSP: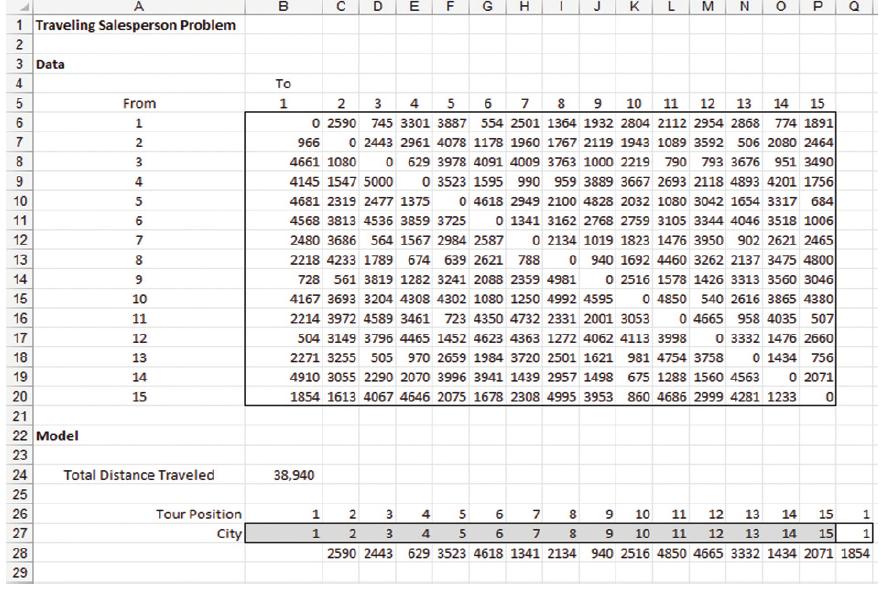

The current solution in row 27 is to simply travel the cities in the order they are numbered. As shown in cell B24, the total distance traveled for this tour is 38,940 miles. For any proposed tour (ordering of the cities in row 27, we use the INDEX function to get the distance between pairs of cities in the tour (note in the following figure we have hidden columns D through P).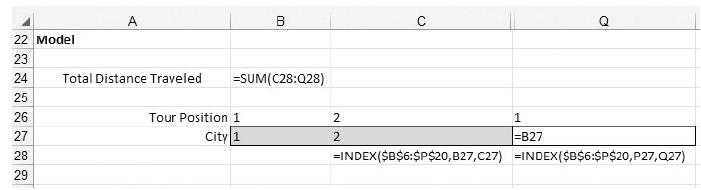

The INDEX function works as follows: 5INDEX($B$6:$P$20,B27,C27) finds the element in the matrix defined by B6:P20 in the row defined by the value in cell B27 and the column defined by the value cell C27. For example, in cell C28 the value returned is the element in the matrix in the first row and the second column, which is 2590. In cell Q27, the formula 5B27 forces the tour to end where it started and the formula in cell B24, 5SUM(C28:Q28) adds up the distances to get the total tour length.

a. Use the Evolutionary method to solve this problem. Minimize B24 with Changing Variable Cells B27:P27, and an All Different constraint for cells B27:P27 (add a constraint and select “dif” as the constraint type). Keep the default options, but set the Random Seed to 15.

Give the best tour found and its total distance.

b. What percentage improvement is gained by the solution found versus the original tour which followed the cities in order of their number?

A 1 Traveling Salesperson Problem 2 3 Data 234 B D E F G H J K L N P D 5 669 7 8 9 10 11 12 7 13 8 14 9 15 10 16 11 17 12 18 13 19 14 20 15 9 10 11 12 13 14 15 745 3301 3887 554 2501 1364 1932 2804 2112 2954 2868 774 1891 0 2443 2961 4078 1178 1960 1767 2119 1943 1089 3592 506 2080 2464 4661 1080 To From 1 2 3 4 5 6 7 8 123456 0 2590 966 0 4145 1547 5000 629 3978 4091 4009 3763 1000 2219 790 793 3676 951 3490 0 3523 1595 990 959 3889 3667 2693 2118 4893 4201 1756 4681 2319 2477 1375 0 4618 2949 2100 4828 2032 1080 3042 1654 3317 684 4568 3813 4536 3859 3725 0 1341 3162 2768 2759 3105 3344 4046 3518 1006 2480 3686 564 1567 2984 2587 0 2134 1019 1823 1476 3950 902 2621 2465 2218 4233 1789 674 639 2621 788 0 940 1692 4460 3262 2137 3475 4800 728 561 3819 1282 3241 2088 2359 4981 0 2516 1578 1426 3313 3560 3046 4167 3693 3204 4308 4302 1080 1250 4992 4595 0 4850 540 2616 3865 4380 2214 3972 4589 3461 723 4350 4732 2331 2001 3053 0 4665 958 4035 507 504 3149 3796 4465 1452 4623 4363 1272 4062 4113 3998 0 3332 1476 2660 2271 3255 505 970 2659 1984 3720 2501 1621 4910 3055 2290 2070 3996 3941 1439 2957 1498 1854 1613 4067 4646 2075 1678 2308 4995 3953 981 4754 3758 0 1434 756 675 1288 1560 4563 0 2071 860 4686 2999 4281 1233 0 21 22 Model 23 222222 24 Total Distance Traveled 38,940 25 26 Tour Position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 27 City 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 28 2590 2443 629 3523 4618 1341 2134 940 2516 4850 4665 3332 1434 2071 1854 29