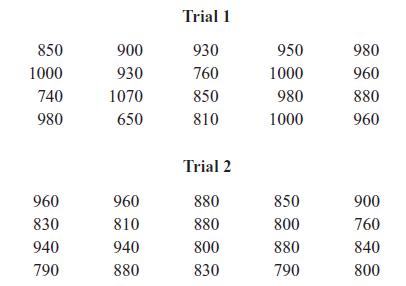
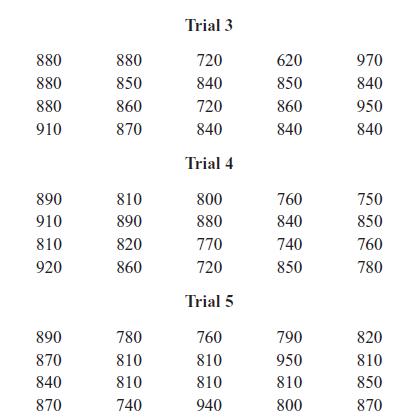
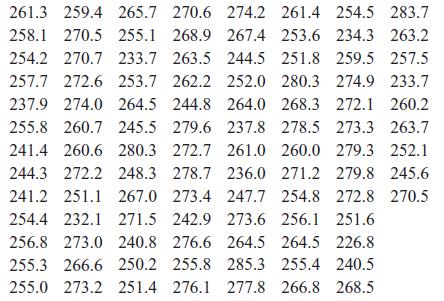
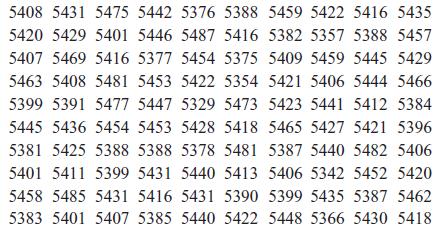
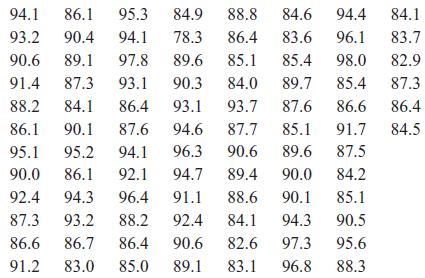
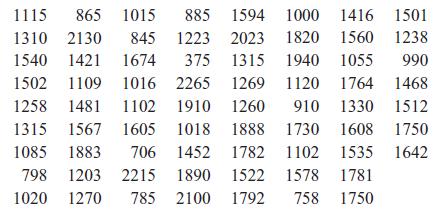
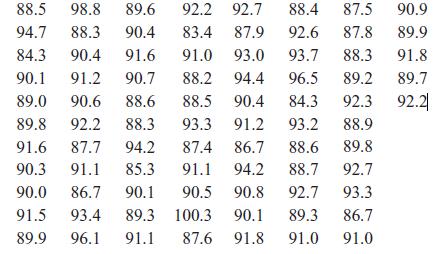
Applied Statistics And Probability For Engineers 3rd Edition Douglas C. Montgomery, George C. Runger - Solutions
Unlock a world of learning with our comprehensive resource for "Applied Statistics And Probability For Engineers 3rd Edition" by Douglas C. Montgomery and George C. Runger. Discover online solutions, answers key, and complete solutions in PDF format, offering step-by-step answers to complex problems. Whether you're looking for the instructor manual, test bank, or chapter solutions, our platform provides everything you need to master this textbook. Access solved problems and questions and answers to enhance your understanding. Enjoy free download options and elevate your study experience with our meticulously curated solution manual.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()