Redo Problem 1.11 to factor the following expressions in which the coefficient of the x2 term now has multiple factors.

(a) 6x2 + 23x + 20

(1) a · b = 6. Factors are [1, 6; 2, 3; 3, 2; 6, 1].

(2) c · d = 20 [1, 20; 2, 10; 4, 5; 5, 4; 10, 2; 20, 1]

(3) ad + bc = 23. Here all the pairs of possible factors from step (2) must be tried with all the possible factors in step (1).

Of all the possible combinations of factors above, only (2 · 4) + (3 · 5) = 23. Carefully arranging the factors, therefore, to ensure that 2 multiplies 4 and 3 multiplies 5, we have

(b) 4x2 + 15x + 14 (1) a · b = 4 [1, 4; 2, 2; 4, 1]
(2) c · d = 14 [1, 14; 2, 7; 7, 2; 14, 1]
(3) ad + bc = 15 [(4 · 2) + (1 · 7) = 15] Arranging the factors to ensure that 4 multiplies 2 and 1 multiplies 7, we have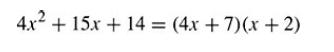

(c) 8x2 + 34x + 21 (1) a · b = 8 [1, 8; 2, 4; 4, 2; 8, 1]
(2) c · d = 21 [1, 21; 3, 7; 7, 3; 21, 1]
(3) ad + bc = 34 [(2 · 3) + (4 · 7) = 34] Arranging the factors so that 2 multiplies 3 and 4 multiplies 7, we have

(d) 6x2 – 17.x + 10 Here with the −17x term, if we wish to limit a and b to positive factors for convenience, c and d must both be negative.
(1) a · b = 6 [1, 6; 2, 3; 3, 2; 6, 1]
(2) c · d = 10 [−1, −10; −2, −5; −5, −2; −10, −1]
(3) ad + bc = −17 [(6 · −2) + (1 · −5) = −17] Arranging the factors so that 6 multiplies −2 and 1 multiplies −5,

(e) 9x2 – 30x + 16 (1) a · b = 9 [1, 9; 3, 3; 9, 1]
(2) c · d = 16 [−1, −16; −2, −8; −4, −4; −8, −2; −16, −1]
(3) ad + bc = −30 [(3 · −8) + (3 · −2) = −30]

Note: Quadratic equations more complicated than this are seldom factored. If factors are needed for solution, the quadratic formula is generally used. See Section 3.5.

Transcribed Image Text:

6x2+23x+20= (2x+5) (3x+4)