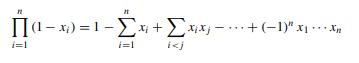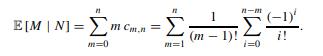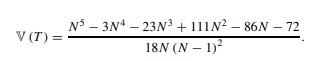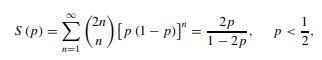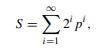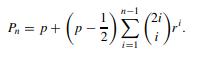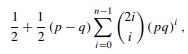Fundamental Probability A Computational Approach 1st Edition Marc S. Paolella - Solutions

Discover comprehensive solutions to the "Fundamental Probability A Computational Approach 1st Edition" by Marc S. Paolella. Access an extensive test bank with expertly solved problems and chapter solutions, providing detailed answers and step-by-step guidance. Our online platform offers a complete answers key and instructor manual for in-depth understanding. Download the solutions PDF for free and explore the textbook's questions and answers with ease. Enjoy the convenience of an online solution manual that enhances your learning experience by offering clear, concise, and reliable solutions to all your probability challenges.