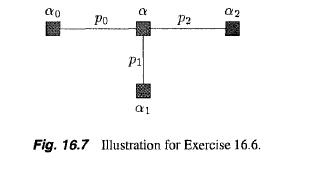
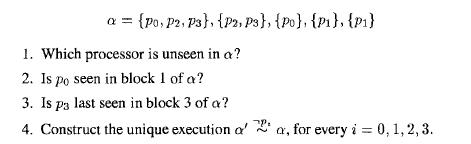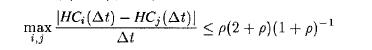Distributed Computing Fundamentals Simulations And Advanced Topics 2nd Edition Hagit Attiya, Jennifer Welch - Solutions
Unlock the comprehensive understanding of "Distributed Computing Fundamentals Simulations And Advanced Topics 2nd Edition" by Hagit Attiya and Jennifer Welch with our expertly-crafted solutions. Access a vast repository of questions and answers, complete with a solution manual that offers detailed, step-by-step answers. Whether you're searching for an instructor manual or a solutions PDF, our resources provide clear, solved problems to enhance your learning experience. Dive into chapter solutions and utilize our test bank for effective study sessions. Discover the convenience of free download options for your textbook needs and ace your exams with our online answers key.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()