Backward elimination is an iterative model selection procedure that begins by considering the model that contains all of the potential independent variables and then attempts to remove independent variables one at a time from this model. On each step, an independent variable is removed from the model if it has the largest p-value of any independent variable remaining in the model and if its p-value is greater than α_stay, an α value for allowing a variable to stay in the model. Backward elimination terminates when all the p-values for the independent variables remaining in the model are less than α_stay. For example, Figure 15.38 shows the MINITAB output of a backward elimination for the residential sales data in Tables 15.17 and 15.19. Here, α_stay has been set equal to .05. Interpret the steps in the output and write out the model that is found by the backward elimination procedure.

Data from Figure 15.38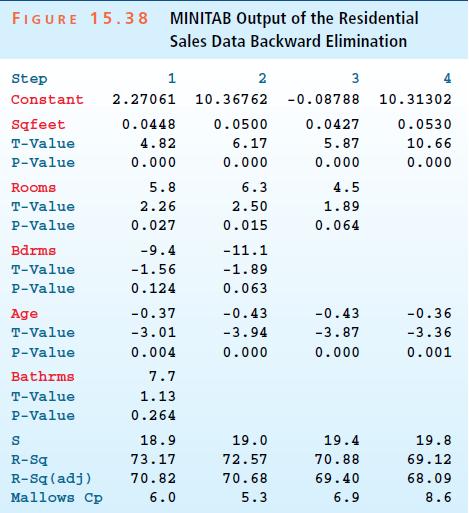

Data from Table 15.17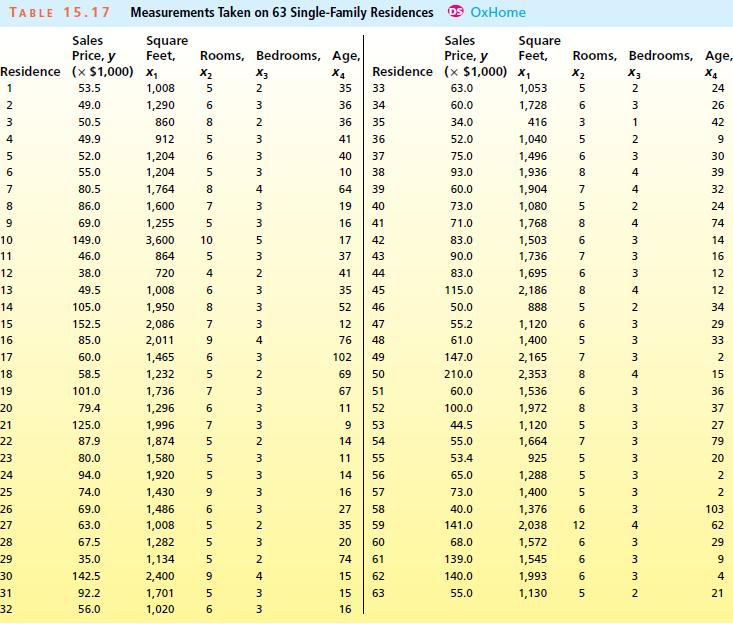

Data from Table 15.19

Transcribed Image Text:

FIGURE 15.38 Rooms T-Value P-Value Bdrms T-Value P-Value Step Constant 2.27061 10.36762 Sqfeet 0.0448 0.0500 T-Value 4.82 6.17 P-Value 0.000 0.000 Age T-Value P-Value Bathrms T-Value P-Value MINITAB Output of the Residential Sales Data Backward Elimination 3 S R-Sq R-Sq (adj) Mallows Cp 1 5.8 2.26 0.027 -9.4 -1.56 0.124 -0.37 -3.01 0.004 7.7 1.13 0.264 2 18.9 73.17 70.82 6.0 6.3 2.50 0.015 -11.1 -1.89 0.063 -0.43 -3.94 0.000 19.0 72.57 70.68 5.3 -0.08788 10.31302 0.0427 0.0530 5.87 10.66 0.000 0.000 4.5 1.89 0.064 -0.43 -3.87 0.000 19.4 70.88 69.40 6.9 -0.36 -3.36 0.001 19.8 69.12 68.09 8.6