A certain college of management has five academic ranks for its faculty: instructor, assistant professor, associate professor, research professor, and applications professor. The first three ranks are tenure-track. Only research professors and applications professors have tenure. A tenure-track faculty member may be discharged, remain at her present rank, or be promoted to the next higher rank. Only tenure-track faculty members can be promoted or discharged. A tenure-track faculty member who is discharged is never rehired. An associate professor may apply for promotion with tenure to the rank of research professor or applications professor. A research professor may remain a research professor or switch to the position of applications professor. Similarly, an applications professor may remain an applications professor or switch to the position of research professor. 

By assigning a state to represent each academic rank, the career path of a faculty member of this college is modeled as a six-state multichain. The state X_n denotes a faculty member’s rank at the end of academic year n. The states are indexed as follows:

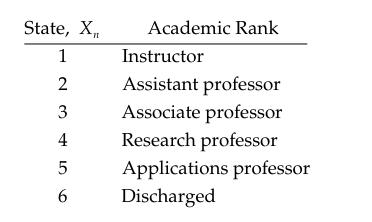
An instructor or assistant professor of rank i will be discharged with probability d_i , remain at her present rank with probability r_i, or be promoted to the next higher rank with probability p_i . An associate professor may be discharged with probability d₃, remain an associate professor with probability r₃, be promoted to the rank of research professor with probability p_R, or be promoted to the rank of applications professor with probability p_A. A research professor may remain a research professor with probability r₄ or switch to the position of applications professor with probability 1 − r₄. Similarly, an applications professor may remain an applications professor with probability r₅ or switch to the position of research professor with probability 1 − r₅.

(a) Construct the transition probability matrix.

(b) Classify the states.

(c) Represent the transition probability matrix in canonical form.  

Transcribed Image Text:

State, X, 1 23456 6 Academic Rank Instructor Assistant professor Associate professor Research professor Applications professor Discharged