An investor buys a stock for \($10\). The monthly share price, rounded to the nearest \($5\), has been varying among \($0\), \($5\), \($10\), \($15\), and \($20\). She has been advised that the price will never exceed \($20\). She has been informed that the price of the stock can be modeled as a recurrent Markov chain in which the state, Xn, denotes the share price at the end of month n. The state space is E = {\($0\), \($5\), \($10\), \($15\), \($20\)}. Her financial advisor believes that the Markov chain will have the following transition probability matrix:

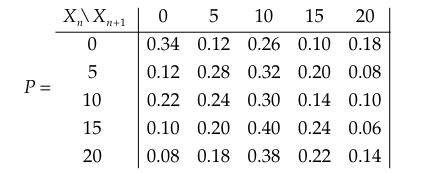
The investor intends to sell the stock at the end of the first month in which the share price rises to \($20\) or falls to \($0\). Under this policy, the share price can be modeled as an absorbing multichain with two absorbing states, \($0\) and \($20\). An absorbing state is reached when the stock is sold. The remaining states, which are entered when the stock is held during the present month, are transient.

(a) Represent the transition probability matrix in canonical form.

(b) Find the probability that she will eventually sell the stock for \($20\).

(c) Find the probability that she will sell the stock after 3 months.

(d) Find the expected number of months until she sells the stock.

Transcribed Image Text:

X\X+1 05 10 15 20 05 0 0.34 0.12 0.26 0.10 0.18 5 P = 10 15 20 0.12 0.28 0.32 0.20 0.08 0.22 0.24 0.30 0.14 0.10 0.10 0.20 0.40 0.24 0.06 0.08 0.18 0.38 0.22 0.14