Consider the following inventory system controlled by a (1, 3) ordering policy. An office supply store sells laptops. The state of the system is the inventory on hand at the beginning of the day. If the number of laptops on hand at the start of the day is less than 1 (in other words, equal to 0), then the store places an order, which is delivered immediately to raise the beginning inventory level to three laptops. If the store starts the day with 1 or more laptops in stock, no laptops are ordered. The number d_n of laptops demanded by customers during day n is an independent, identically distributed random variable which has the following stationary probability distribution:

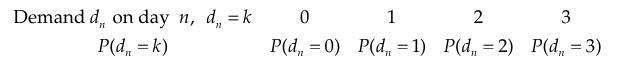
Construct the transition probability matrix for a four-state recurrent Markov chain model of this inventory system under a (1, 3) policy. 

Transcribed Image Text:

Demand d on day n, d = k P(d =k) 0 1 2 3 P(d=0) P(d=1) P(d2) P(d = 3)