The following 8 observations come from a simple linear regression model where the variance ({}^{2}=2^{2}) is known.

The following 8 observations come from a simple linear regression model where the variance \({σ}^{2}=2^{2}\) is known.

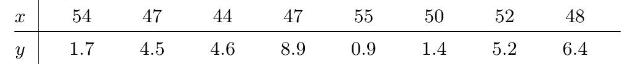
(a) Use BayesLinReg in Minitab, or bayes.lin.reg in R, to nd the posterior distribution of the slope β when we use a \(\operatorname{normal}\left(\begin{array}{lll}0 & 3^{2}\end{array}\right)\) prior for the slope β and a normal \(\left(42^{2}\right)\) prior for the intercept \(x\).
(b) Find a \(95 \%\) Bayesian credible interval for the slope β.
(c) Test the hypothesis \(H_{0}\) : β vs. \(H_{1}:β
(d) Find the predictive distribution of \(y_{9}\) which will be observed at \(x_{9}=\) 51 .
(e) Find a \(95 \%\) credible interval for the prediction.

Transcribed Image Text:

I 54 47 44 47 55 55 50 50 52 48 y 1.7 4.5 4.6 8.9 0.9 1.4 5.2 6.4