Approximate the integral R (x,y) dA by dividing the rectangle R with vertices (0, 0), (4, 0), (4, 2), and (0, 2) into

Approximate the integral
∫_R∫ ƒ(x,y) dA by dividing the rectangle R with vertices (0, 0), (4, 0), (4, 2), and (0, 2) into eight equal squares and finding the sum 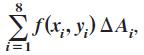where (x_i, y_i) is the center of the ith square. Evaluate the iterated integral and compare it with the approximation.

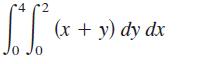
8 .f(x, y) i=1