A curve \(C\) in polar form \(r=f(\theta)\) is parametrized by \(\mathbf{r}(\theta)=(f(\theta) \cos \theta, f(\theta) \sin \theta)\) ) because the \(x\) - and \(y\)-coordinates are given by \(x=r \cos \theta\) and \(y=r \sin \theta\).
(a) Show that \(\left\|\mathbf{r}^{\prime}(\theta)ight\|=\sqrt{f(\theta)^{2}+f^{\prime}(\theta)^{2}}\).
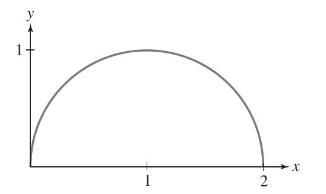
(b) Evaluate \(\int_{C}(x-y)^{2} d s\), where \(C\) is the semicircle in Figure 23 with polar equation \(r=2 \cos \theta, 0 \leq \theta \leq \frac{\pi}{2}\).

Transcribed Image Text:

2 X