As the wheel of radius r cm in Figure 21 rotates, the rod of length L attached

Question:

As the wheel of radius r cm in Figure 21 rotates, the rod of length L attached at point P drives a piston back and forth in a straight line. Let x be the distance from the origin to point Q at the end of the rod, as shown in the figure.

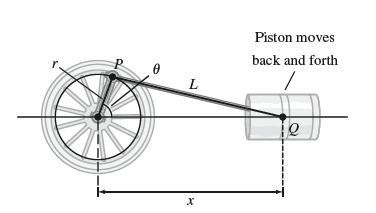
L X Piston moves back and forth Q

(a) Use the Pythagorean Theorem to show that

(b) Differentiate Eq. (1) with respect to t to prove that

Eq.(1)

dh dt || X -0.8- h

2(x-r cos 8) dx dt de + r sin 0- dt do + 2r sin 0 cos 0 = 0

(c) Calculate the speed of the piston when θ = π/2, assuming that r = 10 cm, L = 30 cm, and the wheel rotates at 4 revolutions per minute.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For answer-question

Calculus

ISBN: 9781319055844

4th Edition

Authors: Jon Rogawski, Colin Adams, Robert Franzosa

See More Books

Question Posted: Nov 11, 2023 08:24 AM

You will review both quantitative and qualitative research. The topic is up to you as long as you choose a peer-reviewed, academic research piece. I suggest choosing a topic that is at least in the...
(1) True or false: (a) Angular velocity and linear velocity have the same dimensions. (b) All parts of a rotating wheel must have the same angular velocity. (c) All parts of a rotating wheel must...
The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...
A home buyer bought a house for $245,000. The buyer paid 20 percent down but decided to finance closing costs of 3 percent of the mortgage amount. If the borrower took out a 30-year fixed-rate...
Determine the income participation of Wyatt and Truett, according to each of the five assumptions as to income division listed in Exercise 12-3 if the years net income is $160,000.
Show that the integral in Equation (1) of Example 28.14 has the value RC/2.
James Lewis, a resident of Kentucky, sustained an injury while operating a Caterpillar bulldozer. He filed suit against Caterpillar, a company incorporated in Delaware but with its principal place of...
The following information pertains to Worthy Video Company. 1. Cash balance per bank, July 31, $7,293. 2. July bank service charge not recorded by the depositor $28. 3. Cash balance per books, July...
Why socialism or communism doesn't work in Russia but does in China? as in other countries that we see today. What do you think was the cause of the end of socialism or communism?
"I'll never understand this accounting stuff," Blake Dunn yelled, waving the income statement he had just received from his accountant in the morning mail. "Last month, we sold 1,000 stuffed State...
Let y = tan x. Then y'= sec 2 x and by the Product Rule, y", y"', y = t 2 sin t
Use the Chain Rule to find the derivative. y =cot 9 + 1
Figure P.6.34 shows the distribution of light corresponding to the image arising when a monochromatic point source illuminates two different optical systems each having only one type of aberration....
John's company has assets of $500,000 and owner's equity of $200,000. Calculate John's company's liabilities and income tax
What does reconciling and analysing data help to detect? List any four.
1)List three important principles of economics. 2) Explain in detail why should business owners carefully consider the legal form of ownership for their business? 3) How is the financial risk related...
What is the data relationship throughout the year between profitability and fixed cost? Explain in detail.
Create a server that will wait for a client to connect to it and do the following in order: a.Wait for a password (string) from the client b.Evaluate the string sent by the client according to the...
What effect on sample size does using a greater confidence level have when sampling attribute data?
On March 31, 2018, Gardner Corporation received authorization to issue $30,000 of 9 percent, 30-year bonds payable. The bonds pay interest on March 31 and September 30. The entire issue was dated...
Pr(D) = 0.2, Pr(N) = 0.8, Pr(P | D) = 1.00, and Pr(P | N) = 0.05. Compare with the results in the text, when the disease was much less common. Consider a disease with an imperfect test. Let D denote...
Pr(D) = 0.8, Pr(P | D) = 1.00, and Pr(P | N) = 0.1. Compare with the results in the text and Exercise 37. Consider a disease with an imperfect test. Let D denote the event of an individual having the...
Pr(D) = 0.2, Pr(N) = 0.8, Pr(P | D) = 0.95, and Pr(P | N) = 0.05. Compare your results with Exercise 37. In the above case, the test does not catch every sick person. Let D denote the event of an...
1. In what ways can gathering information about an item, using advertising wisely and comparison shopping help you to be a better consumer? 2. Name four major purchases in which accurate information...
You purchase an RV by making a down payment of $11,400. The terms of your finance agreement have an annual interest rate of 1.91%, compounded monthly, and require you to make 48 monthly payments of...
Problem 1 Monopsony (30 points) 1a. Draw, label, and explain a diagram that shows the effect of a minimum wage on the wage rate, employment, and unemployment in low skilled labor markets if these...

As the wheel of radius r cm in Figure 21 rotates, the rod of length L attached

Question:

L X Piston moves back and forth Q

Step by Step Answer:

a The distance formula gives Thus L xr cos 0 r sin0 Note that L the length of t...View the full answer

Calculus

Students also viewed these Mathematics questions