(Delta) denotes the Laplace operator defined by Prove the identity [ operatorname{curl}(operatorname{curl}(mathbf{F}))=abla(operatorname{div}(mathbf{F}))-Delta mathbf{F} ] where (Delta mathbf{F})...

Question:

\(\Delta\) denotes the Laplace operator defined by

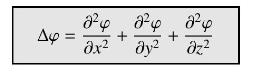
image text in transcribed

Prove the identity
\[
\operatorname{curl}(\operatorname{curl}(\mathbf{F}))=abla(\operatorname{div}(\mathbf{F}))-\Delta \mathbf{F}
\]
where \(\Delta \mathbf{F}\) denotes \(\left\langle\Delta F_{1}, \Delta F_{2}, \Delta F_{3}ightangle\).

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For answer-question

Calculus

ISBN: 9781319055844

4th Edition

Authors: Jon Rogawski, Colin Adams, Robert Franzosa

See More Books

Question Posted: Jan 28, 2024 12:00 AM

See More Questions

\(\Delta\) denotes the Laplace operator defined by Let \(\mathbf{F}=r^{n} \mathbf{e}_{r}\), where \(n\) is any number, \(r=\left(x^{2}+y^{2}+z^{2}ight)^{1 / 2}\), and \(\mathbf{e}_{r}=r^{-1}\langle...
\(\Delta\) denotes the Laplace operator defined by A function \(\varphi\) satisfying \(\Delta \varphi=0\) is called harmonic. (a) Show that \(\Delta \varphi=\operatorname{div}(abla \varphi)\) for any...
\(\Delta\) denotes the Laplace operator defined by Prove the identity = + dx2 +
0.1 M CH3COOH with 0.1 M NH3. The relative conductivities of the solutions tested are as follows: 0.1 M CH3COOH/0.1 M NH3 measured in parallel: (b) 0.1 M CH,COOH with 0.1 M NH,. The relative...
Is system A is in thermal equilibrium with system B, but B is not in thermal equilibrium with system C, What can you say about the temperatures of A, B, and C?
Preston Industrial Supply offers terms of 2/10, n/30 to its wholesale customers. Prestons cost of goods sold is 25% of sales. The company had the following transactions during October: Requirements...
Jack DeCoster owned Quality Egg, LLC, an Iowa egg production company. Jacks son, Peter DeCoster, served as the companys chief operating officer. Jack also owned and operated several egg production...
Tanek Industries manufactures and sells three different models of wet-dry shop vacuum cleaners. Although the shop vacs vary in terms of quality and features, all are good sellers. Tanek is currently...
2. The armadillo is known as one of the world's fastest land animals. On one particular occasion, a biologist observed an armadillo named [N57E] for 6.00 s. The armadillo then ran 19.0 m [N23W]. What...
Let \(\mathcal{S}\) be the boundary surface of a region \(\mathcal{W}\) in \(\mathbf{R}^{3}\), and let \(D_{\mathbf{n}} \varphi\) denote the directional derivative of \(\varphi\), where...
A vector field \(\mathbf{F}\) is incompressible if \(\operatorname{div}(\mathbf{F})=0\) and is irrotational if \(\operatorname{curl}(\mathbf{F})=\mathbf{0}\). Prove that the cross product of two...
Let (x, y) = x cos(y) and x = u 2 + v 2 and y = u v. af af (a) Calculate the primary derivatives x' dy (b) Use the Chain Rule to calculate df/av. Leave the answer in terms of both the dependent and...
Solve the triangle. 3 2 75 3 40
Evaluate the integral. 4/t 1 e4/t 2 dt II 0
Differentiate the function R(q) = q - 5 cos q. R'(q) =
NEED ALL TEST cases TO PASS Import unittest def pyramid_builder(blocks): ''' given a certain number of blocks how many layers of a pyriamid can mr. frog build? a pyramid is built as follows... * -> 1...
In general for a binary gas, we know that at an elevated temperature T and a reduced pressure P, its diffusion coefficient DAB roughly obeys the following scaling relation: DAB & T 73/2 Here, in the...
Explain the random walk model for exchange rate forecasting. Can it be consistent with technical analysis?
Let (x) = x 2 - 9, g(x) = 2x, and h(x) = x - 3. Find each of the following. (((--) 2
Why is the disk method a special case of the general slicing method?
The region R bounded by the graph of y = f(x) 0 and the x-axis on [a, b] is revolved about the line y = -2 to form a solid of revolution whose cross sections are washers. What are the inner and...
Use the general slicing method to find the volume of the following solids. The solid whose base is the region bounded by the curves y = x 2 and y = 2 - x 2 , and whose cross sections through the...
All of the capacitors in the figure below are 6.6 F. What is the equivalent capacitance of this network? 9V
10. Two charges are evenly spaced in 2 cm intervals on the x-axis: q = 10 nC and q = -3 nC. How much work is required to bring a positive charge of q3 = 4 nC from a point at infinity to point A if...
An air-filled capacitor consists of two parallel plates, each with an area of 7.60 cm, separated by a distance of 2.00 mm. If a 16.0 V potential difference is applied to these plates, calculate the...

(Delta) denotes the Laplace operator defined by Prove the identity [ operatorname{curl}(operatorname{curl}(mathbf{F}))=abla(operatorname{div}(mathbf{F}))-Delta mathbf{F} ] where (Delta mathbf{F})...

Question:

0x2 ' ' +

Step by Step Answer:

Calculus

Students also viewed these Mathematics questions