If a bucket of water spins about a vertical axis with constant angular velocity (in radians

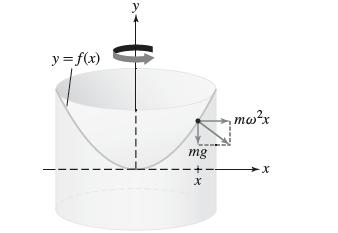
If a bucket of water spins about a vertical axis with constant angular velocity ω (in radians per second), the water climbs up the side of the bucket until it reaches an equilibrium position (Figure 16). Two forces act on a particle located at a distance x from the vertical axis: the gravitational force −mg acting downward and the force of the bucket on the particle (transmitted indirectly through the liquid) in the direction perpendicular to the surface of the water. These two forces must combine to supply a centripetal force mω²x, and this occurs if the diagonal of the rectangle in Figure 16 is normal to the water’s surface (i.e., perpendicular to the tangent line). Prove that if y = ƒ(x) is the equation of the curve obtained by taking a vertical cross section through the axis, then −1/y' = −g/(ω²x). Show that y = ƒ(x) is a parabola.

Transcribed Image Text:

y =f(x) y mg X mw²x →X