In 1535, the mathematician Antonio Fior challenged his rival Niccolo Tartaglia to solve this problem: A tree
Question:
In 1535, the mathematician Antonio Fior challenged his rival Niccolo Tartaglia to solve this problem: A tree stands 12 braccia high; it is broken into two parts at such a point that the height of the part left standing is the cube root of the length of the part cut away. What is the height of the part left standing? Show that this is equivalent to solving x3 + x = 12 and finding the height to three decimal places. Tartaglia, who had discovered the secret of solving the cubic equation, was able to determine the exact answer:
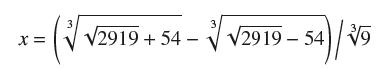
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





