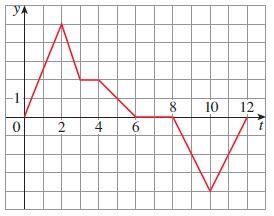
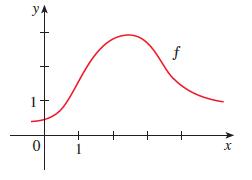
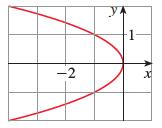
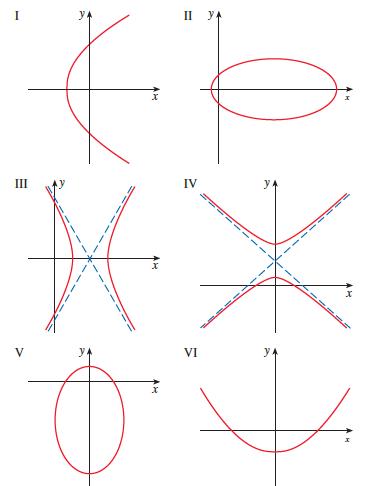
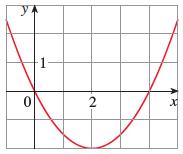
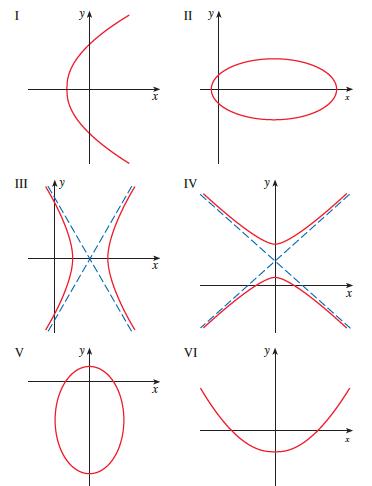
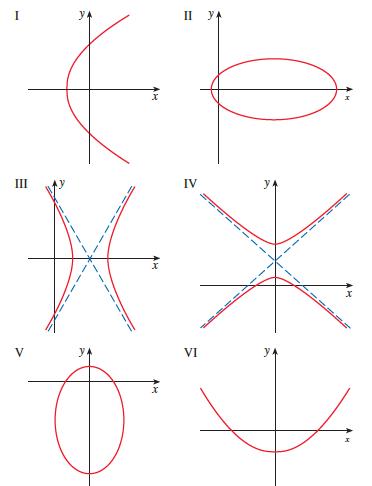
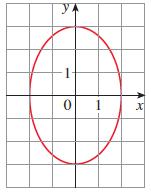
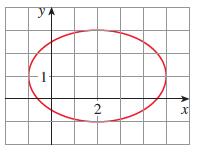
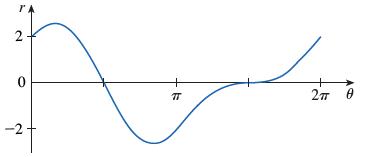
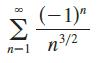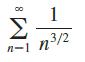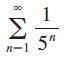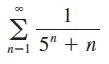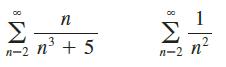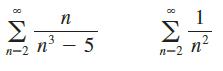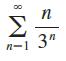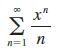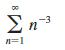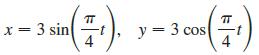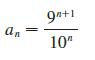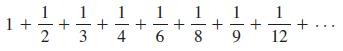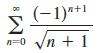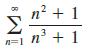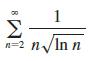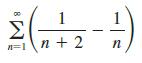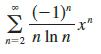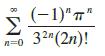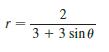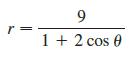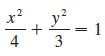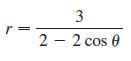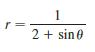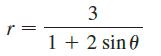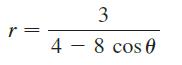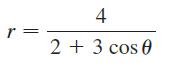Calculus Early Transcendentals 9th Edition James Stewart, Daniel K. Clegg, Saleem Watson, Lothar Redlin - Solutions

Discover comprehensive solutions for "Calculus Early Transcendentals 9th Edition" by James Stewart, Daniel K. Clegg, Saleem Watson, and Lothar Redlin. Our online platform provides an extensive answers key and detailed solutions manual, ideal for students seeking a deep understanding of calculus concepts. Access solutions in PDF format and explore solved problems across various chapters. Whether you're looking for questions and answers, a test bank, or step-by-step answers, our resources are designed to support your learning journey. Benefit from an instructor manual and textbook resources available for free download to enhance your calculus skills.