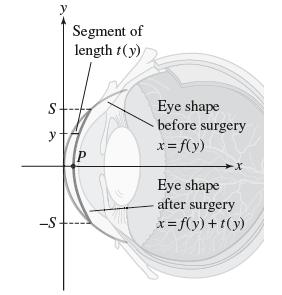
In a recent study of laser eye surgery by Gatinel, Hoang-Xuan, and Azar, a vertical cross section of the cornea is modeled by the half-ellipse of Exercise 69. Show that the half-ellipse can be written in the form x = ƒ(y), where ƒ(y) = p⁻¹ (r − √r² − py²). During surgery, tissue is removed to a depth t(y) at height y for −S ≤ y ≤ S , where t(y) is given by Munnerlyn’s equation (for some R > r):

After surgery, the cross section of the cornea has the shape x = f (y) + t(y) (Figure 20). Show that after surgery, the radius of curvature at the point P (where y = 0) is R.

Transcribed Image Text:

- - t(y) = R - S R y r S + r y -