In Exercise 62 of Section 9.1, we described the tractrix by the differential equation

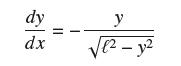
Show that the parametric curve c(t) identified as the tractrix in Exercise 106 satisfies this differential equation. The derivative on the left is taken with respect to x, not t.

Data From Exercise 106

Verify that the tractrix curve (ℓ  > 0)

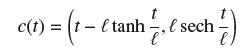
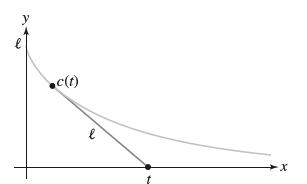
has the following property: For all t, the segment from c(t) to (t, 0) is tangent to the curve and has length ℓ (Figure 28).

Transcribed Image Text:

dy dx || 1 y √12-1² y2