Let a > 0 and n > 1. Define (x) = x n /e ax 1 for x 0 and (0) = 0.

Let a > 0 and n > 1. Define ƒ(x) = xⁿ/e^ax − 1 for x ≠ 0 and ƒ(0) = 0.

(a) Use L’Hôpital’s Rule to show that ƒ is continuous at x = 0.
(b) Show that ∫^∞₀ ƒ(x) dx converges. Show that ƒ(x) ≤ 2^xne^−ax if x is large enough. Then use the Comparison Test and Exercise 93.

Data From Exercise 93

Let Jn = ∫^∞₀ xⁿ e^−αx dx, where n ≥ 1 is an integer and α>0. Prove that

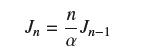
and J₀ = 1/α. Use this to compute J₄. Show that J_n = n!/αⁿ⁺¹.

Jn n -J-1 a