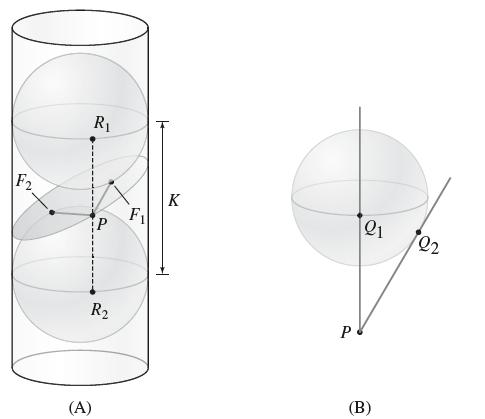
Let C be the curve obtained by intersecting a cylinder of radius r and a plane. Insert two spheres of radius r into the cylinder above and below the plane, and let F₁ and F₂ be the points where the plane is tangent to the spheres [Figure 15(A)]. Let K be the vertical distance between the equators of the two spheres. Rediscover Archimedes’s proof that C is an ellipse by showing that every point P on C satisfies PF₁ + PF₂ = K If two lines through a point P are tangent to a sphere and intersect the sphere at Q₁ and Q₂ as in Figure15(B), then the segments  have equal length. Use this to show that PF₁ = PR₁ and PF₂ = PR₂.

Transcribed Image Text:

PQ1 and PQ2