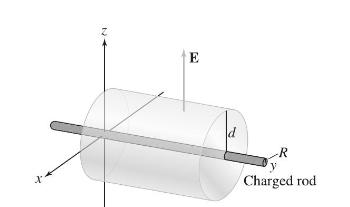
Let \(\mathbf{E}\) be the electric field due to a long, uniformly charged rod of radius \(R\) with charge density \(\delta\) per unit length (Figure 21). By symmetry, we may assume that \(\mathbf{E}\) is everywhere perpendicular to the rod and its magnitude \(E(d)\) depends only on the distance \(d\) to the rod (strictly speaking, this would hold only if the rod were infinite, but it is nearly true if the rod is long enough). Show that \(E(d)=\delta / 2 \pi \epsilon_{0} d\) for \(d>R\). Apply Gauss's Law to a cylinder of radius \(R\) and of unit length with its axis along the rod.

X E -R y Charged rod