Let (mathbf{F}) be the vector field [ mathbf{F}(x, y)=leftlanglefrac{x}{x^{2}+y^{2}}, frac{y}{x^{2}+y^{2}}ightangle ] and assume that (C_{R}) is the

Question:

Let \(\mathbf{F}\) be the vector field
\[
\mathbf{F}(x, y)=\left\langle\frac{x}{x^{2}+y^{2}}, \frac{y}{x^{2}+y^{2}}ightangle
\]
and assume that \(C_{R}\) is the circle of radius \(R\) centered at the origin and oriented counterclockwise.
(a) Show that \(\frac{\partial F_{2}}{\partial x}-\frac{\partial F_{1}}{\partial y}=0\).
(b) Explain why we cannot use Green's Theorem to argue that \(\int_{C_{R}} \mathbf{F} \cdot d \mathbf{r}=0\).
(c) By direct computation of the line integral, show that \(\int_{\mathcal{C}_{R}} \mathbf{F} \cdot d \mathbf{r}=0\).
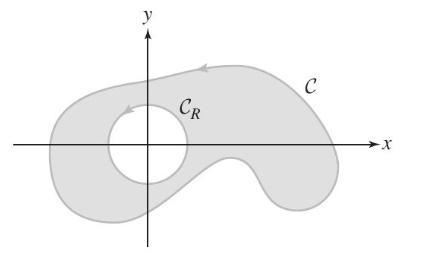
(d) Let \(C\) be the curve shown in Figure 26. Explain why we can use Green's Theorem, along with the result of (c), to conclude that \(\int_{C} \mathbf{F} \cdot d \mathbf{r}=0\).

image text in transcribed