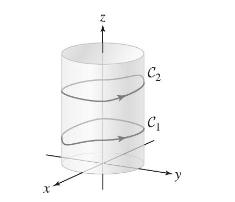
Question: Let (mathbf{F}=leftlangle y^{2}, x^{2}, z^{2}ightangle). Show that [ int_{C_{1}} mathbf{F} cdot d mathbf{r}=int_{C_{2}} mathbf{F} cdot d mathbf{r} ] for any two closed curves going around
Let \(\mathbf{F}=\left\langle y^{2}, x^{2}, z^{2}ightangle\). Show that
\[
\int_{C_{1}} \mathbf{F} \cdot d \mathbf{r}=\int_{C_{2}} \mathbf{F} \cdot d \mathbf{r}
\]
for any two closed curves going around a cylinder whose central axis is the z-axis as shown in Figure 21.
N C C
Step by Step Solution
3.35 Rating (161 Votes )
There are 3 Steps involved in it
The question asks us to show that the line integral of the vector field mathbfFlangle y2 x2 z2 angle around any two closed curves C1 and C2 which enci... View full answer

Get step-by-step solutions from verified subject matter experts


