Let (mathbf{F}=leftlangle-z^{2}, 2 z x, 4 y-x^{2}ightangle), and let (C) be a simple closed curve in the

Question:

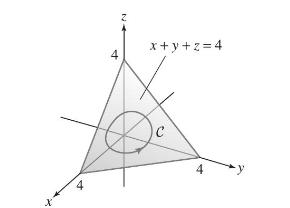
Let $\mathbf{F}=\left\langle-z^{2}, 2 z x, 4 y-x^{2}ightangle$, and let $C$ be a simple closed curve in the plane $x+y+z=4$ that encloses a region of area 16 (Figure 20). Calculate $\oint_{C} \mathbf{F} \cdot d \mathbf{r}$, where $C$ is oriented in the counterclockwise direction (when viewed from above the plane).

image text in transcribed